后缀数组学习笔记
文章目录
【注意】最后更新于 September 22, 2021,文中内容可能已过时,请谨慎使用。
后缀数组是一种处理字符串问题的有力工具(废话),本文的主要特点是一步步地由最朴素的后缀数组构建方法逐步优化,而非直接给出最终优化后的代码。
希望这篇文章能让更多的人看懂后缀数组的代码,学会后缀数组。
本文已于 pr #1730 优化并合并至 OI Wiki,推荐在 OI Wiki 上阅读。
模板题链接
洛谷(只用求 $sa$)
LOJ(只用求 $sa$)
UOJ(求 $sa$ 和 $height$)
评测鸭(求 $sa$ 和 $height$)
两(can)篇(kao)论(zi)文(liao)
[2]:[2009]后缀数组——处理字符串的有力工具 by.罗穗骞
这两篇论文还是写的很好的,大家可以看看。
下文中如果有引用这两篇论文中的内容,将以上标形式标出($^{[1]}$ $^{[2]}$)。
关于字符串..
说到字符串算法,就得先提一些定(fei)义(hua),知道的就可以不看了..
字符集$^{[1]}$
一个字符集 $Σ$ 是一个建立了全序关系的集合,也就是说,$Σ$ 中的任意两个不同的元素 $α$ 和 $β$ 都可以比较大小,要么 $α<β$,要么 $β<α$(也就是$α>β$)。字符集 $Σ$ 中的元素称为字符。
字符串$^{[1]}$
一个字符串 $S$ 是将 $n$ 个字符顺次排列形成的数组,$n$ 称为 $S$ 的长度,表示为 $len(S)$。$S$ 的第 $i$ 个字符表示为 $S[i]$。
子串$^{[1]}$
字符串 $S$ 的子串 $S[i..j],i≤j$,表示 $S$ 串中从 $i$ 到 $j$ 这一段,也就是顺次排列 $S[i],S[i+1],\ldots,S[j]$ 形成的字符串。
后缀
后缀是指从某个位置 $i$ 开始到整个串末尾结束的一个特殊子串。字符串 $S$ 的从 $i$ 开头的后缀表示为 $Suffix(S,i)$,也就是 $Suffix(S,i)=S[i..len(S)]$。$^{[1]}$
下文中以 “后缀 $i$” 代指字符串从 $i$ 开头的后缀。$i$ 称作这个后缀的编号。
字典序
以第 $i$ 个字符作为第 $i$ 关键字进行大小比较,空字符小于字符集内任何字符(即:$a<aa$)。
后缀数组是什么?
后缀数组主要是两个数组:$sa$ 和 $rk$。
其中,$sa[i]$ 表示将所有后缀排序后第 $i$ 小的后缀的编号。$rk[i]$ 表示后缀 $i$ 的排名。
这两个数组满足性质:$sa[rk[i]]=rk[sa[i]]=i$。
后缀数组示例:$^{[2]}$
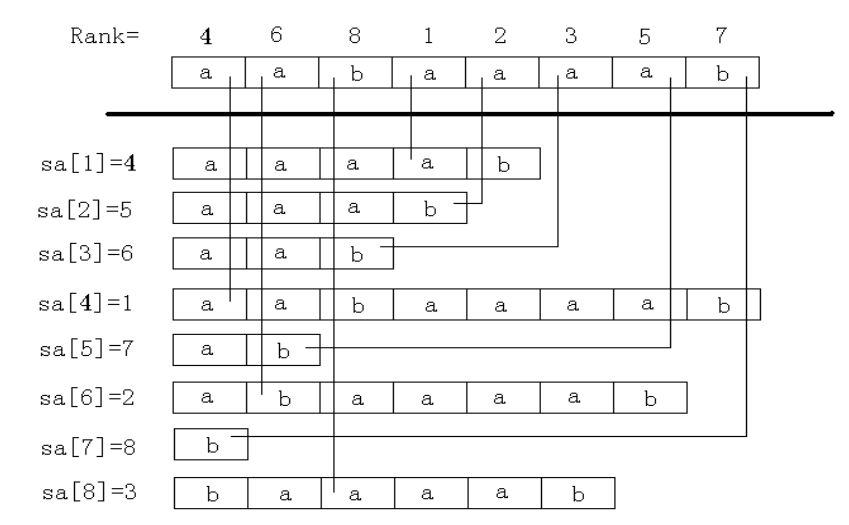
后缀数组怎么求?
$O(n^2\log n)$ 做法
我相信这个做法大家还是能自己想到的..用string+sort就可以了。由于比较两个字符串是 $O(n)$ 的,所以排序是 $O(n^2\log n)$ 的。
$O(n\log^2n)$ 做法
这个做法要用到倍增的思想。
先对每个长度为 $1$ 的子串(即每个字符)进行排序。
假设我们已经知道了长度为 $w$ 的子串的排名 $rk_w[1..n]$(即,$rk_w[i]$ 表示 $s[i..\min(i+w-1,n)]$ 在 $\{s[x..\min(x+w-1,n)]|x\in\mathbb{N}\cap[1,n]\}$ 中的排名),那么,以 $rk_w[i]$ 为第一关键字, $rk_w[i+w]$ 为第二关键字(若 $i+w>n$ 则令 $rk_w[i+w]$ 为 $-INF$)进行排序,就可以求出 $rk_{2w}[1..n]$。
倍增排序示意图:$^{[2]}$
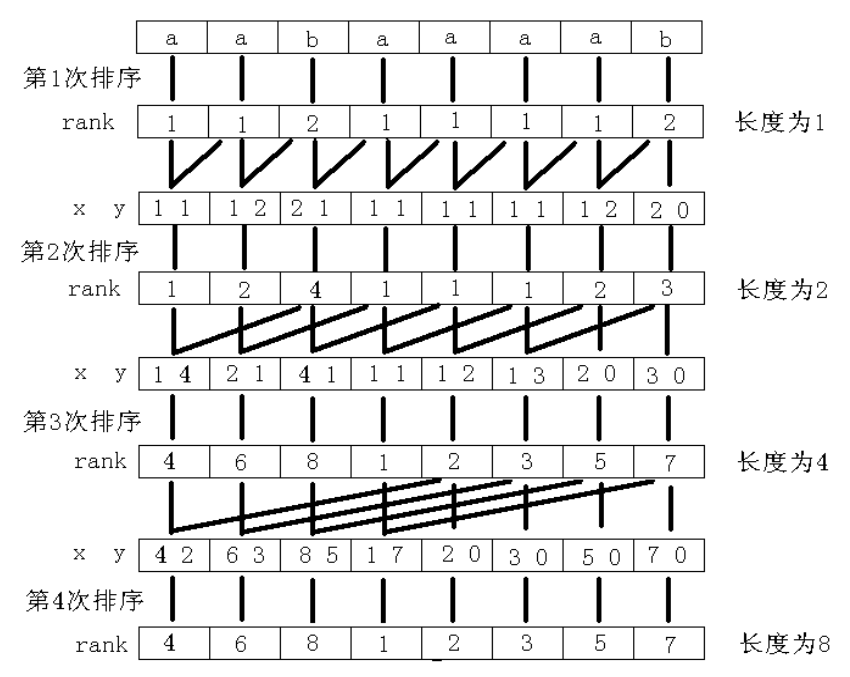
如果用 sort 进行排序,复杂度就是 $O(n\log^2n)$ 的。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1000010;
char s[N];
int n,w,sa[N],rk[N<<1],oldrk[N]; //为了防止访问rk[i+w]导致数组越界,开两倍数组。当然也可以在访问前判断是否越界,但直接开两倍数组方便一些。
int main()
{
int i,p;
scanf("%s",s+1);
n=strlen(s+1);
for (i=1;i<=n;++i) rk[i]=s[i];
for (w=1;w<n;w<<=1)
{
for (i=1;i<=n;++i) sa[i]=i;
sort(sa+1,sa+n+1,[](int x,int y){return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];}); //这里用到了lambda表达式
memcpy(oldrk,rk,sizeof(oldrk)); //由于计算rk的时候原来的rk会被覆盖,要先复制一份
for (p=0,i=1;i<=n;++i) rk[sa[i]]=oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w]?p:++p; //若两个子串相同,它们对应的rk也需要相同,所以要去重
}
for (i=1;i<=n;++i) printf("%d ",sa[i]);
return 0;
}
$O(n\log n)$ 做法
在刚刚的 $O(n\log^2n)$ 做法中,一次排序是 $O(n\log n)$ 的,如果能 $O(n)$ 排序,就能 $O(n\log n)$ 计算后缀数组了。
计数排序
计数排序的核心思想还是比较好理解的,可以先看代码:
//对a这个数组进行排序,结果存到数组b中(b[i]表示第i名的编号),cnt是一个辅助数组,m是a的值域
for (i=1;i<=n;++i) ++cnt[a[i]];
for (i=1;i<=m;++i) cnt[i]+=cnt[i-1];
for (i=n;i>=1;--i) b[cnt[a[i]]--]=i;
其实就是先数一数小于等于 $a[i]$ 的数有多少个,然后从后往前看每个数的名次。感性理解/手玩一下就能明白这个排序算法了。
这个算法有两个特点:
- 它是 $O(n+m)$ 的($m$ 为待排序数据的值域范围)。
- 它是一个稳定排序,即,相等的数会按原位置(下标)进行排序。
基数排序
值得一提的是很多人经常把计数排序和基数排序搞混..
基数排序是一个基于稳定排序的多关键字排序算法,复杂度为关键字个数乘上稳定排序的复杂度。而这个稳定排序通常用计数排序实现。
它的思想是,如果有 $k$ 个关键字,先以第 $k$ 关键字进行一次稳定排序,然后再以第 $k-1$ 关键字进行一次稳定排序,……,最后以第一关键字进行一次稳定排序。可以看出,这样做就完成了以这 $k$ 个关键字的排序。
具体实现大约是这样的:
//key[i][j]表示第j个数的第i关键字,b[i]依然表示第i名的编号,m是key的值域,cnt和id都是辅助数组
for (i=1;i<=n;++i) id[i]=i;
for (i=k;i>=1;--i)
{
memset(cnt,0,sizeof(cnt));
for (j=1;j<=n;++j) id[j]=b[j];
for (j=1;j<=n;++j) ++cnt[key[i][id[j]]];
for (j=1;j<=m;++j) cnt[j]+=cnt[j-1];
for (j=n;j>=1;--j) b[cnt[key[i][id[j]]]--]=id[j];
}
将基数排序运用于求后缀数组
如果你学会了基数排序,也会 $O(n\log^2n)$ 求后缀数组,那你应该可以自己写出一个 $O(n\log n)$ 求后缀数组的程序了。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1000010;
char s[N];
int n,sa[N],rk[N<<1],oldrk[N<<1],id[N],cnt[N];
int main()
{
int i,m,p,w;
scanf("%s",s+1);
n=strlen(s+1);
m=max(n,300);
for (i=1;i<=n;++i) ++cnt[rk[i]=s[i]];
for (i=1;i<=m;++i) cnt[i]+=cnt[i-1];
for (i=n;i>=1;--i) sa[cnt[rk[i]]--]=i;
for (w=1;w<n;w<<=1)
{
memset(cnt,0,sizeof(cnt));
for (i=1;i<=n;++i) id[i]=sa[i];
for (i=1;i<=n;++i) ++cnt[rk[id[i]+w]];
for (i=1;i<=m;++i) cnt[i]+=cnt[i-1];
for (i=n;i>=1;--i) sa[cnt[rk[id[i]+w]]--]=id[i];
memset(cnt,0,sizeof(cnt));
for (i=1;i<=n;++i) id[i]=sa[i];
for (i=1;i<=n;++i) ++cnt[rk[id[i]]];
for (i=1;i<=m;++i) cnt[i]+=cnt[i-1];
for (i=n;i>=1;--i) sa[cnt[rk[id[i]]]--]=id[i];
memcpy(oldrk,rk,sizeof(oldrk));
for (p=0,i=1;i<=n;++i) rk[sa[i]]=oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w]?p:++p;
}
for (i=1;i<=n;++i) printf("%d ",sa[i]);
return 0;
}
一些常数优化
如果你把上面那份代码交到洛谷上..

怎么会这样呢?是这题卡常吗?
一翻其他人的代码,最慢点也不过 $1s$..
这是因为,上面那份代码的常数的确很大..
第二关键字无需计数排序
实际上,像这样就可以了:
for (p=0,i=n;i>n-w;--i) id[++p]=i;
for (i=1;i<=n;++i) if (sa[i]>w) id[++p]=sa[i]-w;
意会一下,先把 $s[i+w..i+2w-1]$ 为空串的位置放前面,再把剩下的按排好的顺序放进去。
优化计数排序的值域
每次对 $rk$ 进行去重之后,我们都计算了一个 $p$,这个 $p$ 即是 $k$ 的值域,将值域改成它即可。
将 $rk[id[i]]$ 存下来,减少不连续内存访问
这个优化在数据范围较大时效果非常明显。
用函数cmp来计算是否重复
同样是减少不连续内存访问,在数据范围较大时效果比较明显。
把 oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w] 替换成 cmp(sa[i],sa[i-1],w),bool cmp(int x,int y,int w){ return id[x]==id[y]&&id[x+w]==id[y+w]; }。
参考代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=1000010;
char s[N];
int n,sa[N],rk[N],oldrk[N<<1],id[N],px[N],cnt[N]; //px[i]=rk[id[i]](用于排序的数组所以叫px)
bool cmp(int x,int y,int w){ return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w]; }
int main()
{
int i,m=300,p,w;
scanf("%s",s+1);
n=strlen(s+1);
for (i=1;i<=n;++i) ++cnt[rk[i]=s[i]];
for (i=1;i<=m;++i) cnt[i]+=cnt[i-1];
for (i=n;i>=1;--i) sa[cnt[rk[i]]--]=i;
for (w=1;w<n;w<<=1,m=p) //m=p就是优化计数排序值域
{
for (p=0,i=n;i>n-w;--i) id[++p]=i;
for (i=1;i<=n;++i) if (sa[i]>w) id[++p]=sa[i]-w;
memset(cnt,0,sizeof(cnt));
for (i=1;i<=n;++i) ++cnt[px[i]=rk[id[i]]];
for (i=1;i<=m;++i) cnt[i]+=cnt[i-1];
for (i=n;i>=1;--i) sa[cnt[px[i]]--]=id[i];
memcpy(oldrk,rk,sizeof(rk));
for (p=0,i=1;i<=n;++i) rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;
}
for (i=1;i<=n;++i) printf("%d ",sa[i]);
return 0;
}
这样优化之后应该不开O2都能过。
$O(n)$ 做法
名字叫DC3,我不会
可以参考[2009]后缀数组——处理字符串的有力工具 by.罗穗骞,里面有介绍这个算法。
一般情况下用倍增法做足常数优化是不会被卡的..
还有个叫“诱导排序”的东西,也是 $O(n)$ 的,听说又好写(相对于 DC3)又快。
后缀数组无需 $height$ 数组的应用
如果用不到 $height$ 数组,一般就是利用 $rk$ 数组对字符串进行排序,有时需要对原串进行一定的加工使需要排序的字符串变成后缀,或者是只需对后缀进行排序便能对需要排序的字符串进行排序。
[JSOI2007]字符加密
[USACO07DEC]Best Cow Line, Gold
$height$ 数组
后缀数组的题目往往是要用到 $height$ 数组的。
lcp(最长公共前缀)
两个字符串 $S$ 和 $T$ 的 $lcp$ 就是最大的 $x$ 使得 $S_i=T_i$ ($\forall 1\le i\le x$) 。
下文中以 $lcp(i,j)$ 表示后缀 $i$ 和后缀 $j$ 的最长公共前缀(的长度)。
$height$ 数组的定义
$height[i]=lcp(sa[i],sa[i-1])$,即第 $i$ 名的后缀与它前一名的后缀的最长公共前缀。
$O(n)$ 求 $height$ 数组需要的一个引理
$height[rk[i]]\ge height[rk[i-1]]-1$
证明的话..感性理解
当 $height[rk[i-1]]\le1$ 时,上式显然成立(右边小于等于 $0$ )。
当 $height[rk[i-1]]>1$ 时:
设后缀 $i-1$ 为 $aAD$($A$ 是一个长度为 $height[rk[i-1]]-1$ 的字符串),那么后缀 $i$ 就是 $AD$。设后缀 $sa[rk[i-1]-1]$ 为 $aAB$ ,那么 $lcp(i-1,sa[rk[i-1]-1])=aA$。由于后缀 $sa[rk[i-1]-1]+1$ 是 $AB$,一定排在后缀 $i$ 的前面,所以后缀 $sa[rk[i]-1]$ 一定含有前缀 $A$,所以 $lcp(i,sa[rk[i]-1])$ 至少是 $height[rk[i-1]]-1$。
简单来说:
$i-1$:$aAD$
$i$:$AD$
$sa[rk[i-1]-1]$:$aAB$
$sa[rk[i-1]-1]+1$:$AB$
$sa[rk[i]-1]$:$A[B/C]$
$lcp(i,sa[rk[i]-1])$:$AX$($X$ 可能为空)
$O(n)$ 求 $height$ 数组的代码实现
利用上面这个引理暴力求即可:
for (i=1,k=0;i<=n;++i)
{
if (k) --k;
while (s[i+k]==s[sa[rk[i]-1]+k]) ++k;
ht[rk[i]]=k; //height太长了缩写为ht
}
利用摊还分析/势能分析可以发现是O(n)的,$k$ 不会超过 $n$,最多减 $n$ 次,所以最多加 $2n$ 次。
应用 $height$ 数组需要的一个性质
$lcp(sa[i],sa[j])=\min\{height[i+1..j]\}$
感性理解:如果 $height$ 一直大于某个数,前这么多位就一直没变过;反之,由于后缀已经排好序了,不可能变了之后变回来。
严格证明可以参考[2004]后缀数组 by.徐智磊。
$height$ 数组的应用
$height$ 数组往往用来解决关于字符串公共部分的题目,通常需要和RMQ/单调栈等算法相结合。

评论正在加载中...如果评论较长时间无法加载,你可以 搜索对应的 issue 或者 新建一个 issue 。