后缀自动机是一种处理字符串问题的有力工具（废话），它的码量不比后缀数组大（实际代码难度不比后缀数组小，但也不难），处理问题时的思维难度往往比后缀数组小，复杂度更优秀。若字符集大小为 $|\Sigma|$，则：构建时间复杂度 $O(n|\Sigma|)$，转移时间复杂度 $O(1)$，空间复杂度 $O(n|\Sigma|)$ 或 构建时间复杂度 $O(n\log|\Sigma|)$，转移时间复杂度 $O(\log|\Sigma|)$，空间复杂度 $O(n)$。

确定有限状态自动机（DFA）

一个 确定有限状态自动机（DFA） 由以下五部分构成：

1. 字符集（$\Sigma$），该自动机只能输入这些字符。
2. 状态集合（$Q$）。如果把一个DFA看成一张有向图，那么 DFA 中的状态就相当于图上的顶点。
3. 起始状态（$start$），$start\in Q$，是一个特殊的状态。起始状态一般用 $s$ 表示，为了避免混淆，本文中使用 $start$。
4. 接受状态集合（$F$），$F\subseteq Q$，是一堆特殊的状态。
5. 转移函数（$\delta$），$\delta$ 是一个接受两个参数返回一个值的函数，其中第一个参数和返回值都是一个状态，第二个参数是字符集中的一个字符。如果把一个DFA看成一张有向图，那么 DFA 中的转移函数就相当于顶点间的边，而每条边上都有一个字符。

DFA 的作用就是识别字符串，一个自动机 $A$，若它能识别（接受）字符串 $S$，那么 $A(S)=True$，否则 $A(S)=False$。

当一个DFA读入一个字符串时，从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态，那么我们称这个 DFA 接受 这个字符串，反之我们称这个 DFA 不接受 这个字符串。

如果一个状态 $v$ 没有字符 $c$ 的转移，那么我们令 $\delta(v,c)=null$，而 $null$ 只能转移到 $null$，且 $null$ 不属于接受状态集合。无法转移到任何一个接受状态的状态都可以视作 $null$，或者说，$null$ 代指所有无法转移到任何一个接受状态的状态。

我们扩展定义转移函数 $\delta$，令其第二个参数可以接收一个字符串：$\delta(v,s)=\delta(\delta(v,s[1]),s[2..|s|])$，这个扩展后的转移函数就可以表示从一个状态起接收一个字符串后转移到的状态。那么，$A(s)=[\delta(start,s)\in F]$。

如，一个接受且仅接受字符串 “a”, “ab”, “aac” 的 DFA：

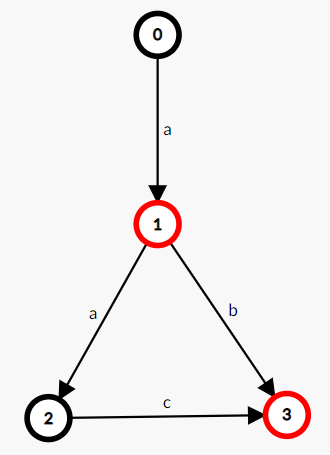
后缀自动机（SAM）

定义

一个字符串的 后缀自动机（SAM） 就是一个 接受且仅接受 这个字符串的 所有后缀 的 DFA。

下文中以 $SAM_s$ 代指字符串 $s$ 的后缀自动机，$\delta_s$ 代指 $SAM_s$ 的转移函数。若不带下标则表示字符串为母串 $s$（需要构建 SAM 的那个字符串）。

根据定义，一个字符串 $t$ 是一个字符串 $s$ 的后缀，当且仅当 $SAM_s(t)=True$。

性质

一个字符串 $t$ 是一个字符串 $s$ 的子串，当且仅当 $\delta_s(start_s,t)\neq null$。

因为，若 $t$ 是 $s$ 的子串，则在 $t$ 之后添加字符可能成为 $s$ 的一个后缀，反之不可能。

一个朴素的SAM

若我们将一个字符串的所有后缀插入到一个字典树（Trie 树）中，并将每次插入的终止节点标记为接受状态，就可以得到一个状态数为 $O(n^2)$ 的SAM。

如，串 “abaaabaa” 的一个 朴素SAM：

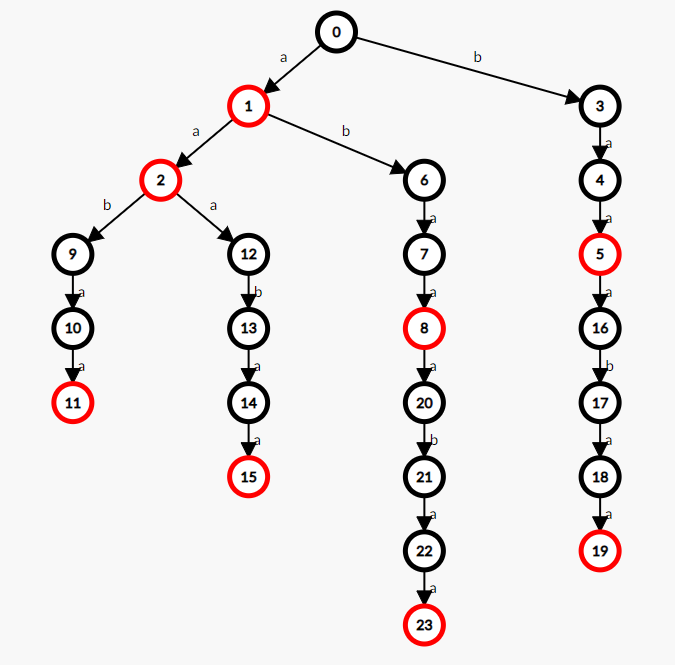
最简SAM

上文中的“朴素SAM”状态数是 $O(n^2)$ 的，而 最简SAM 的状态数和转移数（点数和边数）都是 $O(n)$ 的。

$right$ 集合

对于一个字符串 $t$，若它在 $s$ 中出现的位置集合为：$\{[l_1,r_1),[l_2,r_2),\cdots,[l_n,r_n)\}$（下标从 $0$ 开始），那么定义 $right(t)$ 为 $\{r_1,r_2,\cdots,r_n\}$。

如，又是串 “abaaabaa”，那么 $right(a)=\{1,3,4,5,7,8\}$，$right(aa)=\{4,5,8\}$，$right(aab)=\{6\}$。

在有的教程中，也称其为 $endpos$ 集合。

$right$ 集合等价类

$right$ 集合等价类的定义

$right$ 集合相等的字符串组成一个 $right$ 集合等价类。

如，双是串 “abaaabaa”，那么 $right$ 集合为 $\{4,8\}$ 的字符串有 $\{abaa,baa\}$，这两个字符串组成一个 $right$ 集合等价类。

$right$ 集合等价类与最简SAM

我们定义 $reg(v)$ 表示 从状态 $v$ 开始能识别的字符串的集合。即：$t\in reg(v)$ 当且仅当 $\delta(v,t)\in F$（$F$ 为接受状态集合）。

如果在 $t$ 的后面补上一个字符串 $s[r_i..n]$（$r_i\in right(t)$，$n$ 表示 $s$ 的长度），就得到了 $s$ 的一个后缀。所以，若 $right(t_1)=right(t_2)$，那么 $reg(SAM(t_1))=reg(SAM(t_2))=\{s[r_i..n]|r_i\in right(t_1)\}$。

对于每个状态 $v$，我们只关心 $reg(v)$，所以可以用SAM上的每一个状态去表示一个 $right$ 集合等价类，转移函数也相应地更改为对应的等价类（令 $f(v)$ 表示原状态 $v$ 对应的字符串的 $right$ 集合等价类在最简SAM中对应的状态，那么原来的转移函数 $\delta(u,c)=v$ 更改为 $\delta'(f(u),c)=f(v)$。可以证明，若 $right(u_1)=right(u_2)$，那么 $right(\delta(u_1,c))=right(\delta(u_2,c))$，因为 $right(\delta(u,c))=\{r_i|r_i\in right(u),s[r_i]=c\}$）。

这样的SAM是状态数最少的，因为状态的 $reg$ 两两不同。这样的SAM若要和朴素SAM区分，可以叫做 最简SAM。但一般不加说明的SAM都指最简SAM。

这样的SAM，从起始状态到某个状态可能有多条路径，每条路径都对应一个字符串，那么我们称这个状态 对应 着这些字符串。

如，叒是串 “abaaabaa​” 的最简SAM：

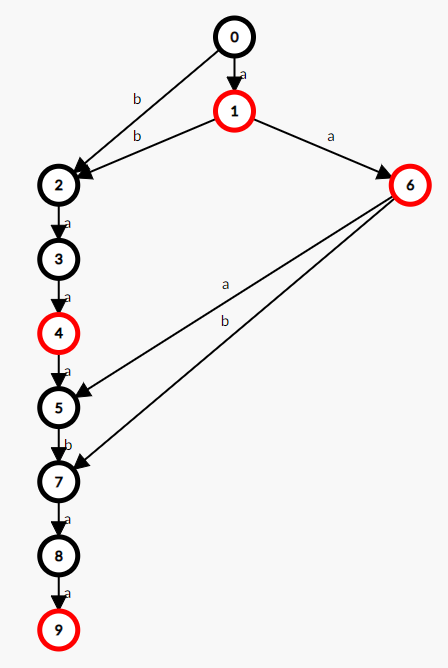
$right$ 集合等价类的性质

对于每个状态 $v$，定义 $max(v)$ 和 $min(v)$ 分别表示 这个状态对应的 最长 和 最短 的字符串。

那么，$v$ 对应的任意一个字符串都是 $max(v)$ 的后缀，且不是 $min(v)$ 的真后缀。并且，$v$ 包含了所有这样的字符串。

第一点（$v$ 中的任意一个字符串都是 $max(v)$ 的后缀）可以由 $right$ 集合的定义得到。

第二点（且不是 $min(v)$ 的真后缀）可以由 $min(v)$ 的定义得到。

第三点（$v$ 包含了所有这样的字符串）可以由一个引理证明：**对于一个字符串 $t$ ，它的 $right$ 集合是它的任意一个后缀的 $right$ 集合的子集。**这个引理很好证明，进而可以证明这条性质。

如，叕是串 “abaaabaa”，$right$ 集合为 $\{6\}$ 的串有 $\{aab,aaab,baaab,abaaab\}$，若这个 $right$ 集合等价类对应状态 $v$，那么 $max(v)=abaaab$，$min(v)=aab$。

这条性质说明 “aaab” 和 “baaab” 都属于这个 $right$ 集合等价类，且 “ab” 和 “b” 不属于这个 $right$ 集合等价类。

证明第三点所用的引理说明，$right(aaab)\subseteq right(aab)\subseteq right(ab)\subseteq right(b)$，也就是 $\{6\}\subseteq\{6\}\subseteq\{2,6\}\subseteq\{2,6\}$ 。

$parent$

$parent$ 的定义

$parent$ 有两种等价的定义（你也可以把其一视作定义，另一个视作性质）：

定义一

对于每个状态 $v$（除了起始状态），找到最长的一个字符串 $t$ 所对应的状态，使得 $right(v)\subsetneq right(t)$（注意是真子集；如果不存在这样的字符串就找起始状态），这样的状态就是 $parent(v)$。

定义二

对于每个状态 $v$（除了起始状态），$min(v)[1..n-1]$ 对应的状态（$n$ 表示 $min(v)$ 的长度，假定空串对应起始状态）就是 $parent(v)$。

有的教程中把 $parent$ 叫做后缀连接 $link$。

$parent$ 的性质

$len(min(v))=len(max(parent(v)))+1$，这个可以由定义二说明。

$parent$ 树

$parent$ 连接可以构成一棵树。

由定义一，由 $right$ 集合要么包含要么不相交可以说明。$parent$ 树可以看成 $right$ 集合的包含关系所构成的树。

由定义一或定义二，由除起始状态外的状态都有且仅有一条出边并且 $parent$ 连接无环（$right$ 集合大小递增/对应字符串长度递减）可以说明。

如，醊是串 “abaaabaa”，它的 $parent$ 树：（用 $max(v)$ 代表每个状态）

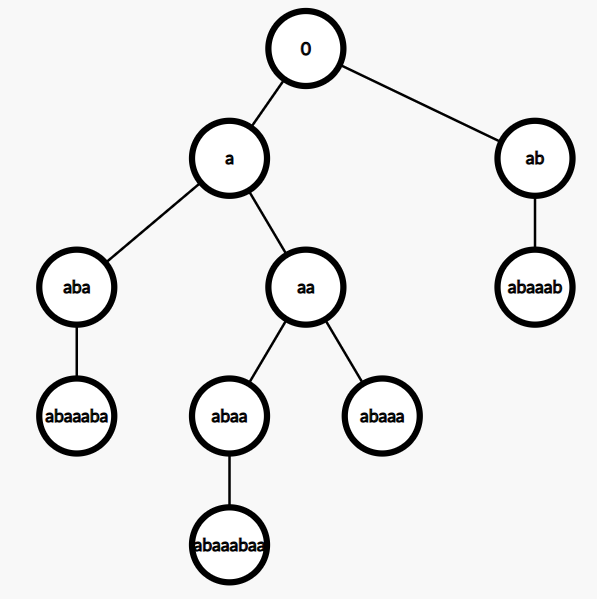
SAM上的接受状态就是包含 $r_i=n$（字符串长度）的一些 $right$ 集合等价类，也就是 $parent$ 树上 $\{n\}$ 对应的状态及其祖先。因此，可以通过 $parent$ 树确定SAM的接受状态集合。

最简SAM状态数为线性的证明

每次把 $right$ 集合分成 $k$ 部分需要 $k$ 条边，最坏情况下每次都只分成两部分，总共要分成至多 $n$ 部分，所以状态数不会超过 $2n-1$（分 $n-1$ 次最多 $2n-2$ 条边，也就是 $2n-1$ 个点）。

最简SAM转移数为线性的证明

考虑SAM的任意一个生成树，那么SAM上的边就会被分成树边和非树边。

树边最多只有 $2n-2$ 条。

对于字符串的每个后缀，将其输入到SAM中都会经过一条终点为接受状态的路径，若经过了一条非树边，则称该后缀对应它经过的 第一条 非树边。

对于每条非树边 $(u,v)$，一定存在一条从起始状态到 $u$ 的不经过任何非树边的路径（因为树上两点间必定有路径），也一定存在一条从 $v$ 到任意一个接受状态的路径（否则 $v=null$），所以，至少有一个后缀对应着这条非树边。

因此，非树边数量不会超过后缀数量。总的边数就是 $O(n)$ 的。

最简SAM的线性构造

SAM的线性构造可以在均摊 $O(1)$ 的时间复杂度内向SAM增加一个字符（从 $SAM_{s[0..i-1]}$ 变成 $SAM_{s[0..i]}$）。

向SAM增加一个字符，就是在所有接受状态后增加一个字符。所以，我们需要考虑上一次插入时的最后一个状态（$last$）以及它在 $parent$ 树上的祖先（也就是所有接受状态）。

加入一个字符 $x$ 时，我们先创建一个新状态 $np$，这个状态刚插入时代表 $right$ 集合 $\{i\}$（$i$ 表示这是插入的第 $i$ 个字符）。

一个引理：若一个状态有字符 $c$ 的转移，则它在 $parent$ 树上的祖先都有。

引理的证明：$right(\delta(v,c))=\{r_i|r_i\in right(v),s[r_i]=c\}$，而 $right(v)\subsetneq right(parent(v))$。

因此，找到 $last$ 最深的有出边 $x$ 的祖先 $p$ 后，在其之上的祖先都有出边 $x$。

对于在其之下的状态，直接向 $np$ 连边即可。

接下来要分三种情况讨论：

若不存在 $p$（起始状态都没有出边 $x$），则将 $parent(np)$ 设为初始状态。

否则，令 $len(v)$ 表示 $max(v)$ 的长度，$q$ 表示 $\delta(p,x)$。

若 $len(q)=len(p)+1$，将 $parent(np)$ 设为 $q$ 即可。

否则，新建状态 $nq$，$len(nq)$ 设为（实际上不是人为设定，它本来就是）$len(p)+1$，将 $q$ 的转移函数复制到 $nq$，然后将 $parent(nq)$ 设为 $parent(q)$，再将 $parent(q)$ 和 $parent(np)$ 都设为 $nq$，最后把 $p$ 及 $p$ 的祖先中所有出边 $x$ 连到 $q$ 的都改为连到 $nq$。实际上，枚举祖先时只要遇到出边 $x$ 不连到 $q$ 的就可以停止枚举了。

至于为什么这样做..恕我表达能力有限，还请参考陈立杰WC课件第 $35$ 页。

构建过程的复杂度证明可以参考 OI-Wiki。

参考代码

#include <cstdio>
#include <cstring>

const int N=1000010;

struct Node
{
    int len,par,ch[26];
} sam[N<<1];

void insert(int x);

char s[N];
int p,tot;

int main()
{
    int i;

    scanf("%s",s);

    sam[0].par=-1;
    for (i=0;s[i];++i) insert(s[i]-'0');

    return 0;
}

void insert(int x)
{
    int np=++tot;
    sam[np].len=sam[p].len+1;
    while (~p&&!sam[p].ch[x])
    {
        sam[p].ch[x]=np;
        p=sam[p].par;
    }
    if (p==-1) sam[np].par=0;
    else
    {
        int q=sam[p].ch[x];
        if (sam[q].len==sam[p].len+1) sam[np].par=q;
        else
        {
            int nq=++tot;
            sam[nq].len=sam[p].len+1;
            memcpy(sam[nq].ch,sam[q].ch,sizeof(sam[q].ch));
            sam[nq].par=sam[q].par;
            sam[q].par=sam[np].par=nq;
            while (~p&&sam[p].ch[x]==q)
            {
                sam[p].ch[x]=nq;
                p=sam[p].par;
            }
        }
    }
    p=np;
}

SAM的一些应用

一些应用我还没有写过..写过之后可能会补（gu）上（gu）来（gu）。可以参考OI wiki。

判断子串/后缀

根据SAM的定义和性质，建出文本串的SAM，将模式串分别输入SAM，若转移到 $null$ 则不是子串，否则是；若转移到接受状态则是后缀，否则不是。

读入字符串时删除首字符

记录一下已读入的字符串长度，若小于等于当前状态的 $parent.len$，就转移到 $parent$。

例题：CF235C Cyclical Quest

子串出现次数

一个子串出现次数就是其对应 $right$ 集合的元素个数。

在创建 $np$ 时，将其 $cnt$ 赋为 $1$，建好SAM后，每个状态的出现次数就是 $parent$ 子树内的 $cnt$ 之和。

例题：【模板】后缀自动机

子串第一次出现位置

和子串出现次数差不多，创建 $np$ 时，将 $firstpos(np)$ 设为 $len(np)-1$，复制 $nq$ 时，将 $firstpos(nq)$ 设为 $firstpos(q)$，最后对子树内取 $min$。

本质不同子串数

每个状态表示 $maxlen-minlen+1$ 个字符串，而 $minlen=len(parent)+1$，所以一个状态表示的字符串数量就是 $len-parent.len$。求和即可。

例题：[SDOI2016]生成魔咒

第 $k$ 大子串

预处理每个状态可以转移到多少个不同的子串，然后就可以做了。

例题：

SP7258 SUBLEX

[TJOI2015]弦论

两串的最长公共子串

对其中一个串建SAM，从起始状态开始，读入另一个字符串，若有转移则转移，将已匹配长度 $+1$，否则跳到 $parent$（这里和 $kmp$ 有点像），并将已匹配长度修改为 $len(parent)$。过程中最大的已匹配长度就是答案。

例题：SP1811 LCS

多串的最长公共子串

还是对其中一个串建SAM，以同样的方式依次读入每个字符串，只不过对每个状态要保存当前字符串的最大匹配长度，所有字符串在某个状态的最大匹配长度的最小值就是这一堆字符串在这个状态能匹配的最大长度。如果能在一个状态匹配，一定能在 $parent$ 处匹配，所以要对子树取 $max$，但也不要忘了对 $len$ 取 $min$。

例题：

SP1812 LCS2

[SDOI2008]Sandy的卡片

任意DFA的压缩

UPD: 这部分内容非常 naive，建议阅读 Wikipedia 或自行搜索易于访问的中文资料，关键词：自动机最小化，Myhill-Nerode 定理。

我就是要看！

这部分估计没人感兴趣..OI里没用，也不是证明SAM最小性必需的（最小性的证明我在前文中已经简略说明了：状态的 $reg$ 两两不同）。只不过或许会对理解SAM本质以及发明它的人怎么想到的有些帮助…

或许这种方式在很多年前就已经被人提出了..总之这部分内容完全是我自己yy的，我也懒得去查有没有人发明过。

这部分内容不保证正确性，如果有误欢迎指正。如果有人愿意提供严谨证明（怎么可能有人啊..只不过我这里都懒得严谨证明了，随便口头地说了一下）一定非常感谢。

“DFA的压缩”的定义

一个可用于压缩DFA的映射 $f:Q_A\rightarrow Q_B$ 需要满足以下几个条件：

1. $\forall v\ne start_A,f(v)\ne f(start_A)$
2. $\forall u\in F,v\notin F,f(u)\ne f(v)$
3. $\forall f(u)=f(v),c\in\Sigma,f(\delta_A(u,c))=f(\delta_A(v,c))$

如：在SAM中，把所有 $right$ 集合相同的状态映射到同一状态就是一个符合条件的映射。

定义DFA $A$ 在映射 $f$ 下的压缩为 $B$，其中：

1. $\Sigma_B=\Sigma_A$
2. $Q_B=f(Q_A)$
3. $start_B=f(start_A)$
4. $F_B=f(F_A)$
5. $\delta_B(f(v),c)=f(\delta_A(v,c))$，这一定义依赖于 $f$ 的性质 $3$。

如：用 $right$ 集合等价类这个映射可以将朴素SAM压缩成最简SAM。

压缩后的自动机与原自动机等价的证明

我们证明一个比 $A(s)=B(s)$ 更强的命题：$[\delta_A(v,s)\in F_A]=[\delta_B(f(v),s)\in F_B]$。

当 $s$ 只有一个字符时，根据 $f$ 满足的性质 $2$ 以及 $B$ 的定义 $4,5$，命题显然成立。

当 $s$ 不止一个字符时，可以归纳地说明命题成立。

DFA的最简压缩方法

这里给出一个将任意DFA压缩至最简的方法：

由于DFA是一个DAG，它的任意生成子图都必定有出度为 $0$ 的点。每次找到这些点，然后从中选取尽量多的点，使其映射到同一个状态后满足 $f$ 需要满足的三条性质（也就是，同一字符转移到的状态映射到的状态相同，且没有一个是接受状态另一个不是的情况），然后将这些点从图中删去，重复直至所有点都有了映射后的状态（所有点都被删去）。这样得到的映射 $f$ 能够将原DFA压缩至最简。

压缩至最简的证明

我们先证明每个状态的 $reg$（定义参见上文，表示从一个状态起能识别的字符串集合）两两不等。我们按照拓扑序归纳地证明。

没有出边的非接受状态可以视作 $null$，而没有出边的接受状态按上文所述方法必定会被映射至同一状态。所以命题对没有出边的状态成立。

假设一个状态所有出边的对应状态都已被证明，那么转移函数不同就等价于 $reg$ 不同，所以命题成立。

接着，我们由 $reg$ 两两不同证明压缩至最简：

若状态数继续减少，那么必然存在原来 $reg$ 不同的两个状态 $B(s_1)$ 和 $B(s_2)$ 被压缩到了一起，任取一个只在 $reg(B(s_1))$ 或只在 $reg(B(s_2))$ 中的字符串 $t$，原来 $B(s_1+t)\ne B(s_2+t)$，压缩后却使得 $B'(s_1+t)=B'(s_2+t)$，不符合要求。