CF603E Pastoral Oddities（结论，LCT/分治+并查集）

题意简述

给你一张边带权且边从 $1$ 到 $m$ 编号的无向图 $G$，称一张图 $H$ 是“好的”，当且仅当存在一个 $H$ 的生成子图 $F$ 使得 $F$ 中每个点的度数都是奇数。现在，你需要回答 $m$ 个问题，第 $i$ 个问题是：求最小的 $x$，使得仅保留 $G$ 中编号不超过 $i$ 且边权不超过 $x$ 的边时，得到的生成子图是“好的”，或者指出不存在这样的 $x$。

$2\le n\le 10^5$, $1\le m\le 3\cdot 10^5$, TL 4s。

简要做法

第一步转化

这道题题意就非常绕口，不转化一下很难下手。

我们需要得到这样一个结论：

$G$ 的一个生成子图是“好的”，当且仅当它的每一个连通块都包含偶数个点。

结论的证明

必要性

如果存在一个连通块有奇数个点，这张图的任何一个生成子图都必然包含一个包含奇数个点的连通块。由于无向图中所有点的度数之和为偶数，一个包含奇数个点的连通块中必然存在度数为偶数的点，从而不符合题意。

充分性

一句话说明：对每个包含偶数个点的连通块找一个生成树，每个点如果有奇数个儿子就断开与父亲的边，就构造出来了。

下面是详细的证明。

先是问题的转化：

需证一张图是“好的”，只需证明它的每一个连通块都是“好的”。

需证一张连通图是“好的”，只需证明它的任意一个生成树都是“好的”。

需证任意一张每个连通块都包含偶数个点的图都是“好的”，只需证明任意一棵包含偶数个点的树都是“好的”。

下面开始证明任意一棵包含偶数个点的树都是“好的”：

首先，任选一个点作为树根。

约定：一个单点的高度是 $1$，树根的所有儿子均是叶子的树高度为 $2$。

接着，使用归纳法证明。

归纳基础：高度为 $2$ 且有偶数个点的树显然是“好的”。高度为 $1$ 或 $2$ 且有奇数个点的树显然有且仅有根的度数为偶数。

归纳假设：高度不超过 $i$ 且有偶数个点的树是“好的”，高度不超过 $i$ 且有奇数个点的树可以通过删边使得有且仅有根的度数为偶数。

归纳证明：

高度为 $i+1$ 且有偶数个点的树是“好的”

删去树根与包含偶数个点的子树之间的连边，由归纳假设得到这些子树都是“好的”，所以只需证明剩下没被删去的部分是“好的”。

删去后，整棵树依然包含偶数个点，因此，根有奇数个儿子，也就是说根的度数为奇数。由归纳假设得到剩下的每棵子树都可以转化成有且仅有根的度数为偶数的树，加上与根相连的这条边，所有子树内的点的度数就都为奇数了。所以，高度为 $i+1$ 且有偶数个点的树是“好的”。
高度为 $i+1$ 且有奇数个点的树可以通过删边使得有且仅有根的度数为偶数。

与上面类似，唯一不同的地方在于删去包含偶数个点的子树后根有偶数个儿子，此时有且仅有根的度数为偶数。

通过上述归纳可以得到，任意一棵包含偶数个点的树都是“好的”，从而充分性得证。

有了这个结论之后，问题就变成了：对于前 $i$ ($1\le i\le m$) 条边，至少要保留其中边权不大于多少的边，才能使得图中所有连通块都包含偶数个点（或者保留所有前 $i$ 条边依然无法满足）。

LCT 做法

考虑按编号顺序加边，用堆/priority_queue 按边权大小维护边，每加一条边就按边权从大到小删边直至出现大小为奇数的连通块，最后删掉的那条边的边权就是答案。由于边权大的边总是先被删掉，可以用 LCT 维护最小生成森林而非整张图。

复杂度 $O(n+m\log n)$ 。

分治做法

这题还有一个神奇的分治做法。

首先，“编号”和“边权”可以看成是两维坐标，从而可以把每条边视作二维平面上的一个点，“编号不超过 $x$ 且边权不超过 $y$ 的边”就对应着 $(0, 0)$ 到 $(x, y)$ 这个矩形。

在下文中，用 $(x_1, y_1, x_2, y_2)$ 表示编号在 $[x_1, x_2]$ 之内，边权在 $[y_1, y_2]$ 之内的所有边构成的集合。

于是，原问题就转变成了，对于每个横坐标 $x$，求出最小的 $y$，使得原图仅保留 $(0, 0, x, y)$ 内的边时，所有连通块都包含偶数个点。

为了方便，下文不考虑无解的情况，写代码时简单判一判就好了。

分治的概述：

全局维护一个支持撤销的并查集。
solve(xl, xr, yl, yr) 会算出 $[xl, xr]$ 的答案，已知这些答案都在 $[yl, yr]$ 内。调用之前需要保证并查集内的边集为 $(0, 0, xl - 1, yl - 1)$。
令 $xmid = (xl + xr) / 2$，solve(xl, xr, yl, yr) 先计算出 $xmid$ 的答案为 $ans[xmid]$，然后递归计算 solve(xl, xmid - 1, ans[xmid], yr) 和 solve(xmid + 1, xr, yl, ans[xmid])。

这带来了两个问题：

递归下去时如何保证并查集内分别含有 $(0, 0, xl-1, ansmid-1)$ 和 $(0, 0, xmid, yl-1)$？
总的时间复杂度是多少？

解决这两个问题前，我们先来看一下更加完整的流程：

solve(xl, xr, yl, yr):
   如果 xl > xr:
      return
   如果 yl = yr:
      [xl, xr] 的答案为 yl
      return
   令此时的并查集状态为 ver1 = (0, 0, xl - 1, yl - 1)
   加上 (xl, 0, xmid, yl - 1) 的边
   令此时的并查集状态为 ver2 = (0, 0, xmid, yl - 1)
   将 (0, yl, xmid, yr) 的边按纵坐标（边权）顺序从小到大加入，直至图中没有奇连通块
   上一步中最后加入的边的边权即为 xmid 的答案 ans[xmid]
   回退至 ver2 = (0, 0, xmid, yl - 1)
   solve(xmid + 1, xr, yl, ans[xmid])
   回退至 ver1 = (0, 0, xl - 1, yl - 1)
   加上 (0, yl, xl - 1, ans[xmid] - 1) 的边，此时并查集内的边为 (0, 0, xl - 1, ansmid - 1)
   solve(xl, xmid - 1, ans[xmid], yr)
   回退至 ver1 = (0, 0, xl - 1, yl - 1)

结合图来理解：

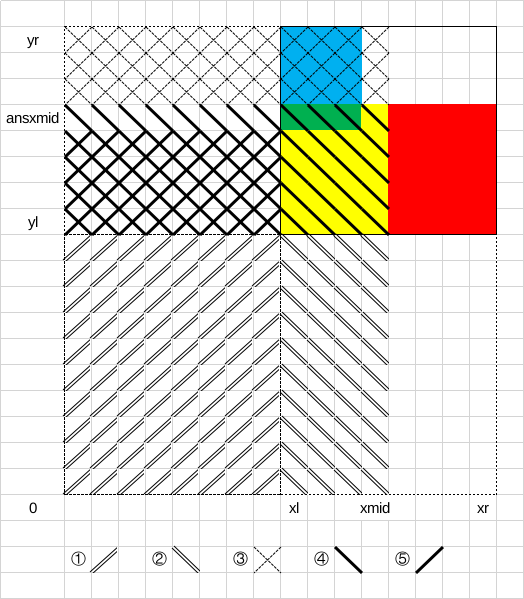
一开始并查集里是 ①。
加上 ②。
在 ③ + ④ 中按边权从小到大加边，直至只有偶连通块。真正加了的边是 ④，ans[xmid] 是 ④ 的顶端。
删掉 ④，递归解决红色部分。
删掉 ②，加上 ⑤，递归解决蓝色部分。

还有一个细节：为了快速获取一个矩形内的边，可以将 $(0, 0, xr, yr)\setminus(0, 0, xl-1, yl-1)$ 这些边作为 solve 的参数。

有了这个完整流程，第一个问题（正确性）解决了。

接下来是第二个问题：时间复杂度是多少？

我们来看每一层分治的 solve 函数的参数构成的的这些矩形，实际上是从左上到右下排列，而 solve 函数中添加/回退/作为参数的边是向左和向下的两条。可以看出：在每一层分治内，每条边最多在三个 solve 函数内带来了常数次操作。（并不会出现多个高度为 $1$ 的矩形排成一排的情况，因为高度为 $1$ 时直接得到答案终止递归了。）

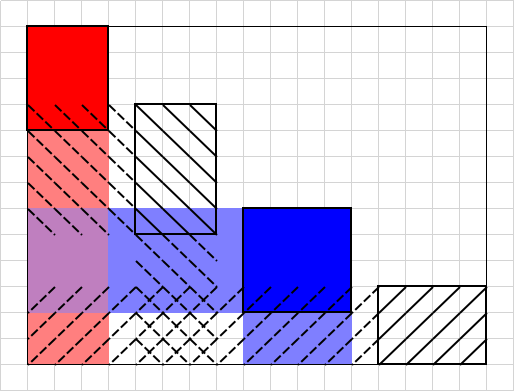
于是，每一层分治的时间复杂度是 $O(m\log n)$，总时间复杂度就是 $O(n+m\log^2 n+m\log m)$。

虽然两个 log，但它是分治和并查集，所以跑的比 LCT 快。

我写的空间复杂度是 $O(n+m\log n)$。貌似可以不在参数里放 $(0, 0, xr, yr)\setminus(0, 0, xl-1, yl-1)$，然后可以线性空间复杂度，不是很懂..（~~如果追求理论复杂度的话 LCT 它不香吗；否则，只要能过，且体会到这个做法的精髓就好。~~）

P.S. 我是在一些常用的数据结构维护手法 - zzq 看到这题和这个做法的（其实是我一开始没看懂他的伪码在干嘛，后来自己想出来的..）。我个人觉得这个和整体二分差的挺大的，套不到整体二分的框架中。但我也不知道整体二分有没有一个官方而精确的定义，大家各自的定义或狭义或广义，读者可以自行判断是否要把这个做法视作一种整体二分。（把这个视作整体二分的人多半会认为决策单调性优化 DP 那个分治也是整体二分吧..）

参考代码

LCT 做法

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cctype>
#include <algorithm>

using namespace std;

const int INF = 2e9;

int read()
{
	int out = 0;
	char c;
	while (!isdigit(c = getchar()));
	for (; isdigit(c); c = getchar()) out = out * 10 + c - '0';
	return out;
}

struct Edge
{
	int u, v, w, id;
	bool operator<(const Edge &b) const
	{
		return w < b.w;
	}
};

struct LCT
{
	struct Node
	{
		vector<int> ch;
		int pa;
		bool node, odd, vir, rev;
		Edge e, mx;
		Node() : ch(2, 0), pa(0), node(true), odd(true), vir(false), rev(false), e({0, 0, 0, 0}), mx({0, 0, 0, 0}) {}
		Node(int u, int v, int w, int id) : ch(2, 0), pa(0), node(false), odd(false), vir(false), rev(false), e({u, v, w, id}), mx({u, v, w, id}) {}
	};
	
	int odd;
	vector<Node> t;
	
	LCT(int n, int m)
	{
		t.resize(n + 1);
		t[0] = Node(0, 0, 0, 0);
		t.reserve(n + m + 1);
		odd = n;
	}
	
	bool nroot(int x)
	{
		return x == t[t[x].pa].ch[0] || x == t[t[x].pa].ch[1];
	}
	
	void pushup(int x)
	{
		t[x].mx = max(t[x].e, max(t[t[x].ch[0]].mx, t[t[x].ch[1]].mx));
		t[x].odd = t[t[x].ch[0]].odd ^ t[t[x].ch[1]].odd ^ t[x].vir ^ t[x].node;
	}
	
	void rotate(int x)
	{
		int y = t[x].pa;
		int z = t[y].pa;
		int k = x == t[y].ch[1];
		if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
		t[x].pa = z;
		t[y].ch[k] = t[x].ch[k ^ 1];
		t[t[x].ch[k ^ 1]].pa = y;
		t[x].ch[k ^ 1] = y;
		t[y].pa = x;
		pushup(y);
		pushup(x);
	}
	
	void reverse(int x)
	{
		swap(t[x].ch[0], t[x].ch[1]);
		t[x].rev ^= 1;
	}
	
	void pushdown(int x)
	{
		if (t[x].rev)
		{
			reverse(t[x].ch[0]);
			reverse(t[x].ch[1]);
			t[x].rev = false;
		}
	}
	
	void Splay(int x)
	{
		static vector<int> stk; // 一件玄学的事是这里 vector 1.7s, stack 2.8s...
		int u = x;
		stk.push_back(x);
		while (nroot(u)) stk.push_back(u = t[u].pa);
		while (!stk.empty())
		{
			pushdown(stk.back());
			stk.pop_back();
		}
		while (nroot(x))
		{
			int y = t[x].pa;
			int z = t[y].pa;
			if (nroot(y)) (x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? rotate(x) : rotate(y);
			rotate(x);
		}
	}
	
	void access(int x)
	{
		for (int y = 0; x; x = t[y = x].pa)
		{
			Splay(x);
			t[x].vir ^= t[y].odd ^ t[t[x].ch[1]].odd;
			t[x].ch[1] = y;
			pushup(x);
		}
	}
	
	void makeroot(int x)
	{
		access(x);
		Splay(x);
		reverse(x);
	}
	
	int findroot(int x)
	{
		access(x);
		Splay(x);
		while (t[x].ch[0])
		{
			pushdown(x);
			x = t[x].ch[0];
		}
		Splay(x);
		return x;
	}
	
	void link(int x, int y, int w, int id)
	{
		int e = t.size();
		t.emplace_back(x, y, w, id);
		makeroot(x);
		makeroot(y);
		odd -= t[x].odd + t[y].odd;
		t[x].pa = t[y].pa = e;
		t[e].vir = t[x].odd ^ t[y].odd;
		pushup(e);
		odd += t[e].odd;
	}
	
	void cut(int x, int y, int id)
	{
		makeroot(x);
		if (findroot(y) == x)
		{
			if (t[t[x].ch[1]].e.id == id || t[t[t[x].ch[1]].ch[0]].e.id == id)
			{
				odd -= t[x].odd;
				t[x].ch[1] = t[y].pa = t[y].ch[0] = 0;
				pushup(x);
				pushup(y);
				odd += t[x].odd + t[y].odd;
			}
		}
	}
};

int main()
{
	int n = read();
	int m = read();
	
	LCT t(n, m);
	
	priority_queue<Edge> q;
	
	int ans = INF;
	
	for (int i = 1; i <= m; ++i)
	{
		int u = read();
		int v = read();
		int w = read();
		q.push({u, v, w, i});
		t.makeroot(u);
		if (t.findroot(v) == u)
		{
			Edge e = t.t[u].mx;
			if (e.w > w)
			{
				t.cut(e.u, e.v, e.id);
				t.link(u, v, w, i);
			}
			else if (!t.odd) ans = min(ans, w);
		}
		else t.link(u, v, w, i);
		
		while (!t.odd)
		{
			Edge e = q.top();
			q.pop();
			ans = min(ans, e.w);
			t.cut(e.u, e.v, e.id);
		}
		
		printf("%d\n", ans == INF ? -1 : ans);
	}
	
	return 0;
}

分治做法

#include <iostream>
#include <cstdio>
#include <cctype>
#include <stack>
#include <vector>
#include <algorithm>

using namespace std;

int read()
{
	int out = 0;
	char c;
	while (!isdigit(c = getchar()));
	for (; isdigit(c); c = getchar()) out = out * 10 + c - '0';
	return out;
}

const int INF = 1e9 + 1;

struct UFS
{
	int odd;
	vector<int> f, s;
	
	struct Change
	{
		int x, y, s;
	};
	stack<Change> c;
	
	void init(int n)
	{
		f.resize(n + 1, 0);
		s.resize(n + 1, 1);
		
		for (int i = 1; i <= n; ++i) f[i] = i;
		odd = n;
	}
	
	int find(int x)
	{
		return x == f[x] ? x : find(f[x]);
	}
	
	void merge(int x, int y)
	{
		x = find(x);
		y = find(y);
		if (x == y) return;
		if (s[x] < s[y]) swap(x, y);
		c.push({x, y, s[x]});
		if ((s[x] & 1) && (s[y] & 1)) odd -= 2;
		s[x] += s[y];
		f[y] = x;
	}
	
	void rollback(int x)
	{
		while ((int)c.size() > x)
		{
			Change t = c.top();
			c.pop();
			if ((t.s & 1) && (s[t.y] & 1)) odd += 2;
			s[t.x] = t.s;
			f[t.y] = t.y;
		}
	}
	
	int status() const { return c.size(); }
} ufs;

struct Edge
{
	int u, v, w, id;
	bool operator<(const Edge &b) const
	{
		return w < b.w;
	}
	bool in(int x1, int y1, int x2, int y2) const
	{
		return id >= x1 && id <= x2 && w >= y1 && w <= y2;
	}
};

vector<int> ans;

void solve(int xl, int xr, int yl, int yr, vector<Edge>& e)
{
	if (xl > xr) return;
	if (yl == yr)
	{
		for (int i = xl; i <= xr; ++i) ans[i] = yl;
		return;
	}
	int ver1 = ufs.status();
	int xmid = (xl + xr) >> 1;
	int p;
	for (p = 0; p < (int)e.size() && e[p].w < yl; ++p)
		if (e[p].in(xl, 0, xmid, yl - 1)) ufs.merge(e[p].u, e[p].v);
	int ver2 = ufs.status();
	for (int i = p; i < (int)e.size(); ++i)
	{
		if (e[i].in(0, yl, xmid, yr))
		{
			ufs.merge(e[i].u, e[i].v);
			if (!ufs.odd)
			{
				ans[xmid] = e[i].w;
				break;
			}
		}
	}
	vector<Edge> le, re;
	for (auto x : e) if (x.in(0, 0, xr, ans[xmid]) && !x.in(0, 0, xmid, yl - 1)) re.push_back(x);
	for (auto x : e) if (x.in(0, 0, xmid - 1, yr) && !x.in(0, 0, xl - 1, ans[xmid] - 1)) le.push_back(x);
	ufs.rollback(ver2);
	solve(xmid + 1, xr, yl, ans[xmid], re);
	if (ans[xmid] < INF)
	{
		ufs.rollback(ver1);
		for (int i = p; i < (int)e.size(); ++i)
			if (e[i].in(0, yl, xl - 1, ans[xmid] - 1)) ufs.merge(e[i].u, e[i].v);
		solve(xl, xmid - 1, ans[xmid], yr, le);
	}
	ufs.rollback(ver1);
}

int main()
{
	int n = read();
	int m = read();
	
	vector<Edge> e;
	
	for (int i = 0; i < m; ++i)
	{
		int u = read();
		int v = read();
		int w = read();
		e.push_back({u, v, w, i});
	}
	
	sort(e.begin(), e.end());
	
	ans.resize(m, INF);
	
	ufs.init(n);
	
	solve(0, m - 1, 1, INF, e);
	
	for (auto x : ans) printf("%d\n", x == INF ? -1 : x);
	
	return 0;
}

文章目录

简要做法

第一步转化

LCT 做法

分治做法

参考代码