Codeforces Round #564 中文题解
文章目录
【注意】最后更新于 September 20, 2020,文中内容可能已过时,请谨慎使用。
2A Nauuo and Votes
题意
$x$ 个人 upvote,$y$ 个人 downvote,$z$ 个人随机 upvote / downvote,问最后总计 up 的多 / down 的多 / up = down / 结果不确定。
题解
考虑两种极端情况:
- 所有随机投的人都 upvote。
- 所有随机投的人都 downvote。
如果这两种情况结果一样,结果就是答案;否则结果不确定。
参考代码
#include <iostream>
using namespace std;
const char result[4] = {'+', '-', '0', '?'};
int solve(int x, int y)
{
return x == y ? 2 : x < y;
}
int main()
{
int x, y, z;
cin >> x >> y >> z;
cout << result[solve(x + z, y) == solve(x, y + z) ? solve(x, y) : 3];
return 0;
}
2B Nauuo and Chess
题意
在一个 $m\times m$ 的棋盘上放 $n$ 颗棋子,第 $i$ 颗棋子的坐标为 $(r_i,c_i)$,需要满足 $|r_i-r_j|+|c_i-c_j|\ge|i-j|$,求 $m$ 的最小值以及任意一种摆放方案。
题解
-
$m\ge\left\lfloor\frac n 2\right\rfloor+1$
$\because\begin{cases}|r_1-r_n|+|c_1-c_n|\ge n-1\\|r_1-r_n|\le m-1\\|c_1-c_n|\le m-1\end{cases}$
$\therefore m-1+m-1\ge n-1$
$\therefore m\ge\frac{n+1}2$
$\because m\text{是整数}$
$\therefore m\ge\left\lfloor\frac n 2\right\rfloor+1$
-
$m$ 可以取到 $\left\lfloor\frac n 2\right\rfloor+1$
在每一斜行放一颗棋子即可,即:$r_i+c_i=i+1$。因为 $|r_i-r_j|+|c_i-c_j|\ge|r_i+c_i-r_j-c_j|$。
参考代码
#include <cstdio>
using namespace std;
int main()
{
int n, i, ans;
scanf("%d", &n);
ans = n / 2 + 1;
printf("%d", ans);
for (i = 1; i <= ans; ++i) printf("\n%d 1", i);
for (i = 2; i <= n - ans + 1; ++i) printf("\n%d %d", ans, i);
return 0;
}
1A Nauuo and Cards
题意
$n$ 张带标号的牌和 $n$ 张空白牌,$n$ 张在手上剩下在牌堆里(牌堆有序),每次可以从手上选一张牌放牌堆底部并从牌堆顶部抽一张牌,需要使牌堆从上到下递增地放 $1$ ~ $n$,求最小操作数。
$1\le n\le2\times10^5$。
题解
首先尝试不打空白牌能否直接完成。如果能就是最优解,否则最优解一定是先打若干空白牌然后再也不打空白牌。计 $p_i$ 为 $i$ 在牌堆的初始位置(初始在手上为 $0$),那么答案为 $\max\limits_{i = 1}^n(p_i - i + 1 + n)$(每张牌最早在第 $p_i + 1$ 张被打出,还要打 $n-i$ 张)。
参考代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, a[N], b[N], p[N], ans;
int main()
{
int i, j;
scanf("%d", &n);
for (i = 1; i <= n; ++i)
{
scanf("%d", a + i);
p[a[i]] = 0;
}
for (i = 1; i <= n; ++i)
{
scanf("%d", b + i);
p[b[i]] = i;
}
if (p[1])
{
for (i = 2; p[i] == p[1] + i - 1; ++i);
if (p[i - 1] == n)
{
for (j = i; j <= n && p[j] <= j - i; ++j);
if (j > n)
{
printf("%d", n - i + 1);
return 0;
}
}
}
for (i = 1; i <= n; ++i) ans = max(ans, p[i] - i + 1 + n);
printf("%d", ans);
return 0;
}
1B Nauuo and Circle
题意
圆上画一 $n$ 点树,树给定,边要求直而不交,画法与排列一一对应,求方案数。
$2\le n\le 2\times10^5$。
题解
首先,如果选一个根使其变为有根树,可以发现每棵子树一定在一段连续的弧上。
考虑 DP,令 $f_u$ 为子树 $u$ 方案数,那么 $f_u=(|son(u)| + [u\ne root])!\prod\limits_{v\in son(u)}f_v$,$ans = nf_{root}$。(先固定根的位置,每棵子树要为儿子排位置,如果非根自己也要参与排位置,然后再画子树。)
事实上不需要 DP,答案为每个点的度数阶乘之积乘上 $n$。
参考代码
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int N = 200010;
const int mod = 998244353;
int n, ans, d[N];
int main()
{
int i, u, v;
scanf("%d", &n);
ans = n;
for (i = 1; i < n; ++i)
{
scanf("%d%d", &u, &v);
ans = (ll) ans * (++d[u]) % mod * (++d[v]) % mod;
}
cout << ans;
return 0;
}
1C Nauuo and Pictures
题意
给你一个长度为 $n$ 的数列 $w_{1..n}$,其中有一些位置是"被喜欢的",其它位置是“不被喜欢的”,进行 $m$ 次操作,每次随机选一个数,选到第 $i$ 个数的概率是 $\frac{w_i}{\sum_{j=1}^nw_j}$,如果选到一个“被喜欢的”位置,就会把这个位置上的数加一,否则减一。问 $m$ 次操作过后每个数的期望值,对 $998244353$ 取模。
$1\le n\le2\times 10^5$,$1\le m\le3000$。
题解
裸dp
先只看一个“被喜欢的”位置,这个位置的初始值是 $w$。
计 $SA$ 为“被喜欢的”数之和,$SB$ 为“不被喜欢的”数之和。
令 $f_w[i][j][k]$ 表示:现在 $SA=j$,$SB=k$,一个值为 $w$ 、“被喜欢的”位置经过 $i$ 次操作后的期望值。
边界情况:$f_w[0][j][k]=w$。
转移:
- 下一次操作选到了当前这个位置。概率:$\frac w{j+k}$。转移到:$f_{w+1}[i-1][j+1][k]$。
- 下一次操作选到了另一个“被喜欢的”位置。概率:$\frac{j-w}{j+k}$。转移到:$f_w[i-1][j+1][k]$。
- 下一次操作选到了一个“不被喜欢的”位置。概率:$\frac k{j+k}$。转移到:$f_w[i-1][j][k-1]$。
所以,$f_w[i][j][k]=\frac w{j+k}f_{w+1}[i-1][j+1][k]+\frac{j-w}{j+k}f_w[i-1][j+1][k]+\frac k{j+k}f_w[i-1][j][k-1]$。
令 $g_w[i][j][k]$ 表示“不被喜欢的”的对应状态,计算方式类似。
这样大约能过简单版。
优化
有两个优化:
-
$f_w[i][j][k]=wf_1[i][j][k]$
证明:
$i=0$ 时显然成立。
假设已经证明了 $f_w[i-1][j][k]=wf_1[i-1][j][k]$,就可以归纳地证明 $f_w[i][j][k]=wf_1[i][j][k]$:
$\begin{aligned}f_1[i][j][k]&=\frac 1{j+k}f_2[i-1][j+1][k]+\frac{j-1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\\&=\frac2{j+k}f_1[i-1][j+1][k]+\frac{j-1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\\&=\frac{j+1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\end{aligned}$
$\begin{aligned}f_w[i][j][k]&=\frac w{j+k}f_{w+1}[i-1][j+1][k]+\frac{j-w}{j+k}f_w[i-1][j+1][k]+\frac k{j+k}f_w[i-1][j][k-1]\\&=\frac{w(w+1)}{j+k}f_1[i-1][j+1][k]+\frac{w(j-w)}{j+k}f_1[i-1][j+1][k]+\frac {wk}{j+k}f_1[i-1][j][k-1]\\&=\frac{w(j+1)}{j+k}f_1[i-1][j+1][k]+\frac {wk}{j+k}f_1[i-1][j][k-1]\\&=wf_1[i][j][k]\end{aligned}$
还有一个比较简单但不那么严谨的理解方式:每一步期望的增量都与期望成正比。(这里被 _rqy 喷了,出题人就是菜,这个证明写不严谨。)
这样的话就只用计算 $f_1[i][j][k]$ 了。
-
注意到 $i$, $j$, $k$, $m$ 有一些联系。实际上可以令 $f'_w[i][j]$ 表示 $f_w[m-i-j][SA+i][SB-j]$(这里的 $SA$ 和 $SB$ 都是未操作时的初始值)。
令 $g'_1[i][j]$ 表示 $g_w[m-i-j][SA+i][SB-j]$,计算方式类似。
总结
$$ \begin{aligned} f'_1[i][j]&=1&(i+j=m)\\ f'_1[i][j]&=\frac{SA+i+1}{SA+SB+i-j}f'_1[i+1][j]+\frac{SB-j}{SA+SB+i-j}f'_1[i][j+1]&(i+j<m)\\ g'_1[i][j]&=1&(i+j=m)\\ g'_1[i][j]&=\frac{SA+i}{SA+SB+i-j}g'_1[i+1][j]+\frac{SB-j-1}{SA+SB+i-j}g'_1[i][j+1]&(i+j<m) \end{aligned} $$
“被喜欢的”位置答案是 $w_if'_1[0][0]$,“不被喜欢的”位置答案是 $w_ig'_1[0][0]$。
如果每次去算逆元就是 $\mathcal O(n+m^2\log p)$,预处理出来就是 $\mathcal O(n+m^2+m\log p)$。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 200010;
const int M = 3010;
const int mod = 998244353;
int qpow(int x, int y) //calculate the modular multiplicative inverse
{
int out = 1;
while (y)
{
if (y & 1) out = (ll) out * x % mod;
x = (ll) x * x % mod;
y >>= 1;
}
return out;
}
int n, m, a[N], w[N], f[M][M], g[M][M], inv[M << 1], sum[3];
int main()
{
int i,j;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; ++i) scanf("%d", a + i);
for (i = 1; i <= n; ++i)
{
scanf("%d", w + i);
sum[a[i]] += w[i];
sum[2] += w[i];
}
for (i = max(0, m - sum[0]); i <= 2 * m; ++i) inv[i] = qpow(sum[2] + i - m, mod - 2);
for (i = m; i >= 0; --i)
{
f[i][m - i] = g[i][m - i] = 1;
for (j = min(m - i - 1, sum[0]); j >= 0; --j)
{
f[i][j] = ((ll) (sum[1] + i + 1) * f[i + 1][j] + (ll) (sum[0] - j) * f[i][j + 1]) % mod * inv[i - j + m] % mod;
g[i][j] = ((ll) (sum[1] + i) * g[i + 1][j] + (ll) (sum[0] - j - 1) * g[i][j + 1]) % mod * inv[i - j + m] % mod;
}
}
for (i = 1; i <= n; ++i) printf("%d\n", int((ll) w[i] * (a[i] ? f[0][0] : g[0][0]) % mod));
return 0;
}
1D Nauuo and Portals
题意
在一个 $n\times n$ 的网格里放传送门,指定从第 $i$ 行进从第 $r_i$ 行出,从第 $i$ 列进从第 $c_i$ 列出,$r_{1..n}$ 和 $c_{1..n}$ 都是排列,求方案。
题解
考虑一个 $n*n$ 的问题如何转化成 $(n-1)\times(n-1)$:满足第一行和第一列。
如果已经满足直接变成 $(n-1)\times(n-1)$。
否则找到第一行中应该放在第一列那个和第一列中应该放在第一行那个,这两个位置各放一个传送门即可。
这题可以 $\mathcal O(n)$ 做,但 checker 要 $\mathcal O(n^2)$。
参考代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1010;
struct Portal
{
int x, y, p, q;
Portal(int _x, int _y, int _p, int _q): x(_x), y(_y), p(_p), q(_q) {}
};
vector<Portal> ans;
int n, a[N], b[N], c[N], d[N], ra[N], rb[N], rc[N], rd[N];
int main()
{
int i;
scanf("%d", &n);
for (i = 1; i <= n; ++i)
{
scanf("%d", b + i);
rb[b[i]] = i;
}
for (i = 1; i <= n; ++i)
{
scanf("%d", a + i);
ra[a[i]] = i;
}
for (i = 1; i <= n; ++i) c[i] = d[i] = rc[i] = rd[i] = i;
for (i = 1; i < n; ++i)
{
if (c[i] == ra[i] && d[i] == rb[i]) continue;
ans.push_back(Portal(i, rc[ra[i]], rd[rb[i]], i));
int t1 = c[i];
int t2 = d[i];
swap(c[i], c[rc[ra[i]]]);
swap(d[i], d[rd[rb[i]]]);
swap(rc[ra[i]], rc[t1]);
swap(rd[rb[i]], rd[t2]);
}
printf("%d\n", ans.size());
for (auto k : ans) printf("%d %d %d %d\n", k.x, k.y, k.p, k.q);
return 0;
}
1E Nauuo and ODT
题意
给你一棵 $n$ 个点,点有颜色的树。一条简单路径的权值是其上颜色数,求所有简单路径的权值之和(路径有序,即 $u\rightarrow v$ 和 $v\rightarrow u$ 算两条)。带修,$m$ 次单点颜色修改,每修改一次输出一次。
$n,m\le 4\times10^5$,$7.5s$。
题解
对每种颜色分别考虑不含该颜色的简单路径条数。
令当前处理的颜色为 $c$,把颜色为 $c$ 的视为白色,不是 $c$ 的视为黑色,那么不含 $c$ 的路径条数就是每个黑联通块的大小的平方和,修改就是当颜色是 $c$ $\leftrightarrow$ 颜色不是 $c$ 时翻转一个点的颜色。所以,问题转化成了黑白两色的树,单点翻转颜色,维护黑联通块大小的平方和。这个转化后的问题可以用很多数据结构做,比如:lxl:top tree 随便维护。这篇题解里使用 Link/cut Tree.
对每个点维护子树大小,儿子大小平方和,在 link/cut 的时候更新答案即可。有一个大家熟知的 trick,就是每个黑点向父亲连边,这样真正的联通块就是 Link/cut Tree 里的联通块删掉根。
具体看图吧,图讲的挺清楚的:
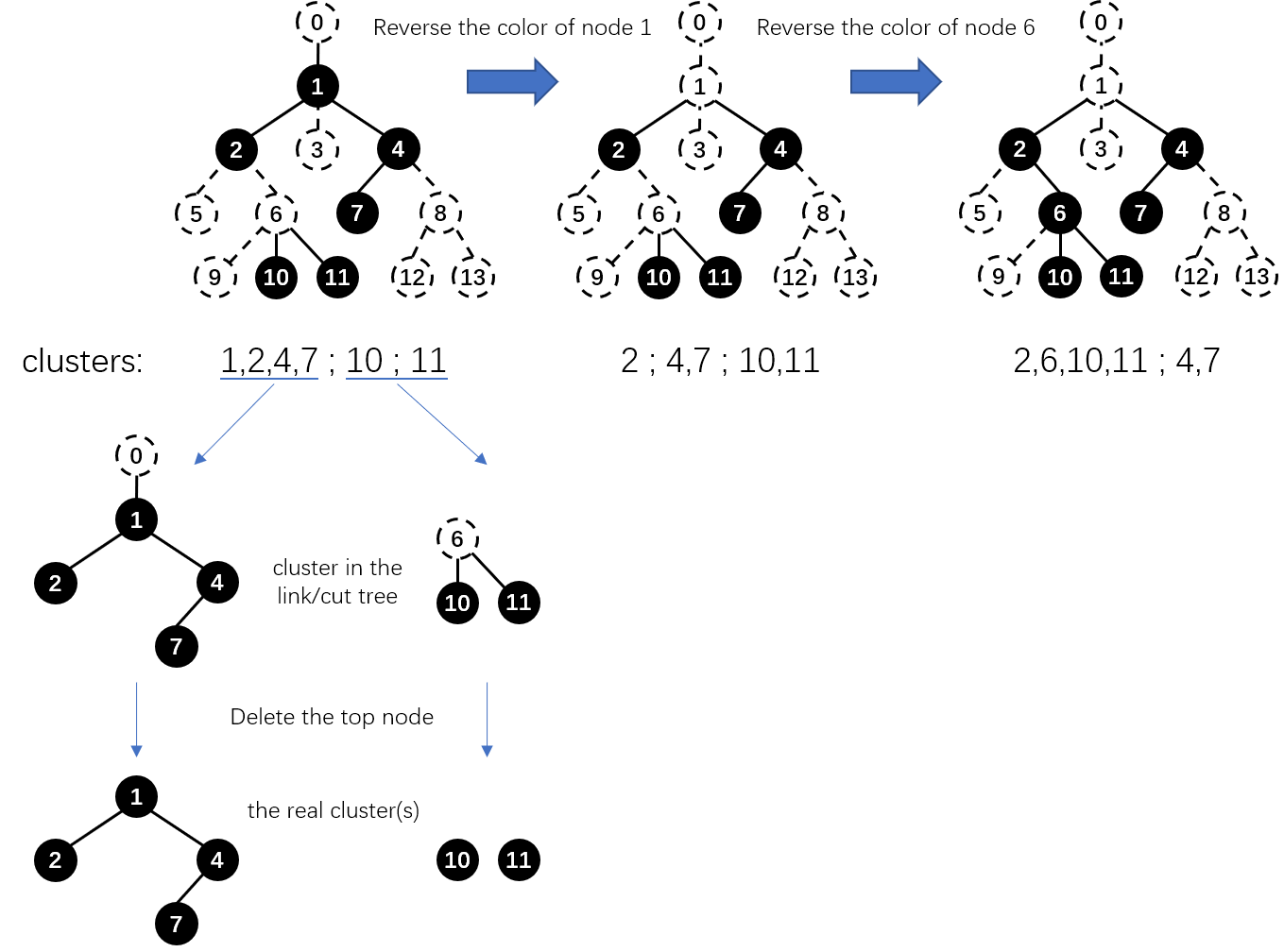
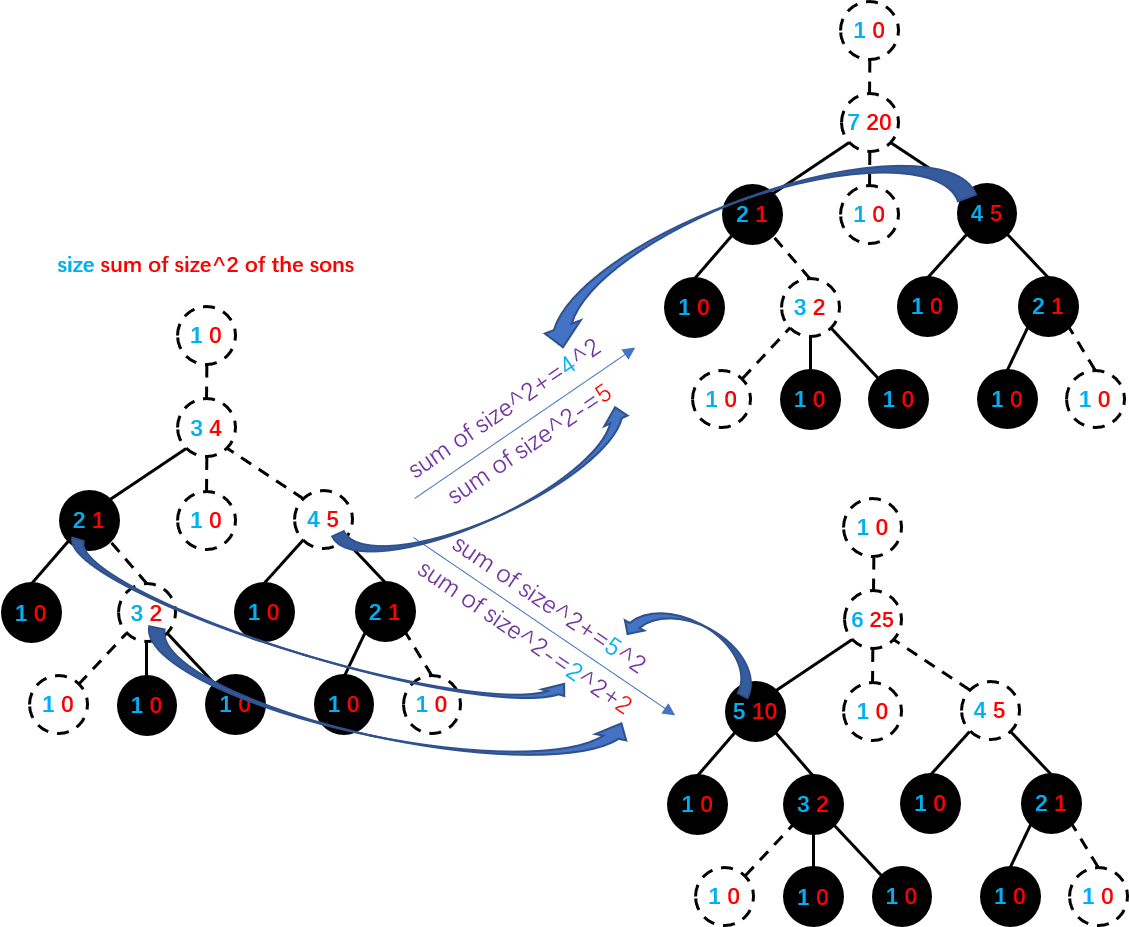
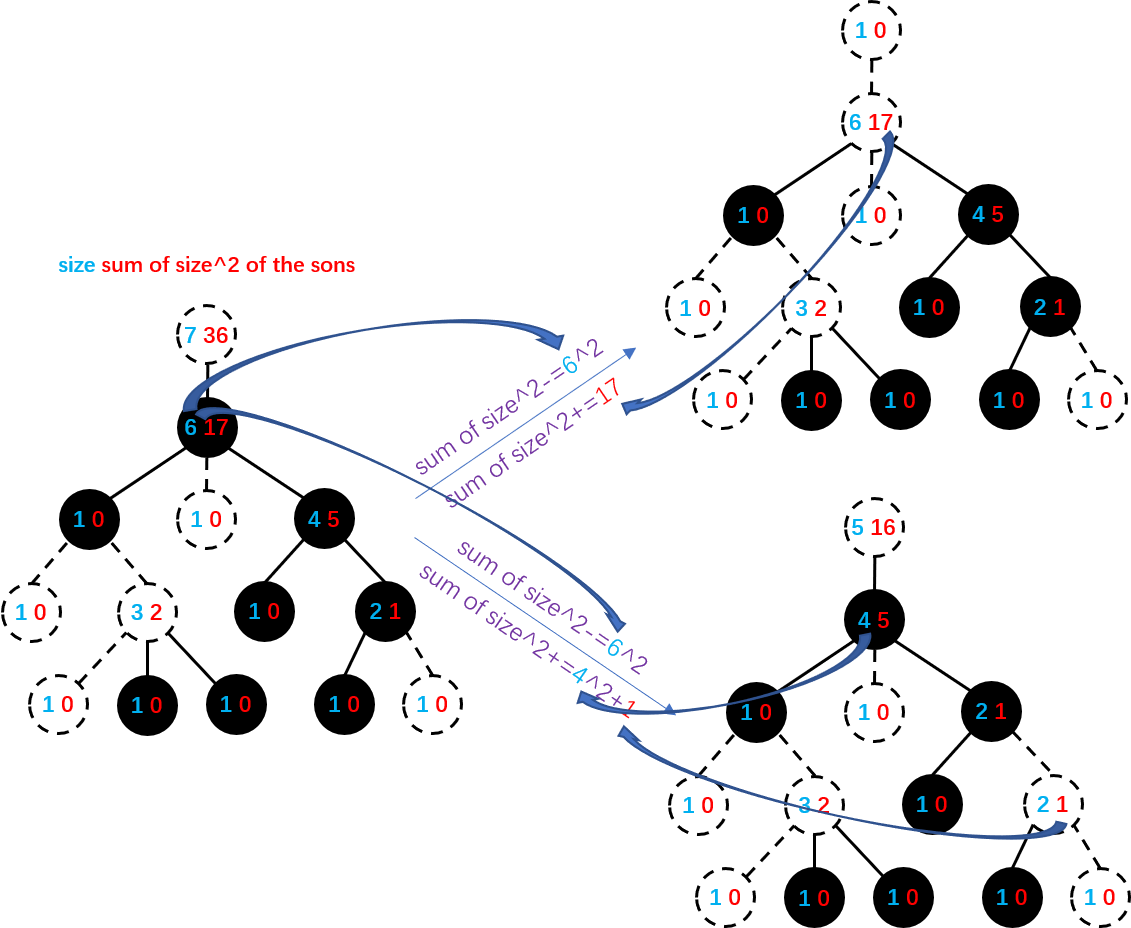
LCT 的部分就是这样,计算答案的时候先初始化一个全是黑点的树,离线处理每个颜色,处理完一个颜色反着改回去。
参考代码
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 400010;
struct Node
{
int fa, ch[2], siz, sizi;
ll siz2i;
ll siz2() { return (ll) siz * siz; }
} t[N];
bool nroot(int x);
void rotate(int x);
void Splay(int x);
void access(int x);
int findroot(int x);
void link(int x);
void cut(int x);
void pushup(int x);
void add(int u, int v);
void dfs(int u);
int head[N], nxt[N << 1], to[N << 1], cnt;
int n, m, c[N], f[N];
ll ans, delta[N];
bool bw[N];
vector<int> mod[N][2];
int main()
{
int i, j, u, v;
ll last;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; ++i)
{
scanf("%d", c + i);
mod[c[i]][0].push_back(i);
mod[c[i]][1].push_back(0);
}
for (i = 1; i <= n + 1; ++i) t[i].siz = 1;
for (i = 1; i < n; ++i)
{
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
for (i = 1; i <= m; ++i)
{
scanf("%d%d", &u, &v);
mod[c[u]][0].push_back(u);
mod[c[u]][1].push_back(i);
c[u] = v;
mod[v][0].push_back(u);
mod[v][1].push_back(i);
}
f[1] = n + 1;
dfs(1);
for (i = 1; i <= n; ++i) link(i);
for (i = 1; i <= n; ++i)
{
if (!mod[i][0].size())
{
delta[0] += (ll)n * n;
continue;
}
if (mod[i][1][0])
{
delta[0] += (ll)n * n;
last = (ll)n * n;
}
else last = 0;
for (j = 0; j < mod[i][0].size(); ++j)
{
u = mod[i][0][j];
if (bw[u] ^= 1) cut(u);
else link(u);
if (j == mod[i][0].size() - 1 || mod[i][1][j + 1] != mod[i][1][j])
{
delta[mod[i][1][j]] += ans - last;
last = ans;
}
}
for (j = mod[i][0].size() - 1; ~j; --j)
{
u = mod[i][0][j];
if (bw[u] ^= 1) cut(u);
else link(u);
}
}
ans = (ll) n * n * n;
for (i = 0; i <= m; ++i)
{
ans -= delta[i];
printf("%I64d ", ans);
}
return 0;
}
bool nroot(int x) { return x == t[t[x].fa].ch[0] || x == t[t[x].fa].ch[1]; }
void rotate(int x)
{
int y = t[x].fa;
int z = t[y].fa;
int k = x == t[y].ch[1];
if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
t[x].fa = z;
t[y].ch[k] = t[x].ch[k ^ 1];
t[t[x].ch[k ^ 1]].fa = y;
t[x].ch[k ^ 1] = y;
t[y].fa = x;
pushup(y);
pushup(x);
}
void Splay(int x)
{
while (nroot(x))
{
int y = t[x].fa;
int z = t[y].fa;
if (nroot(y)) (x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? rotate(x) : rotate(y);
rotate(x);
}
}
void access(int x)
{
for (int y = 0; x; x = t[y = x].fa)
{
Splay(x);
t[x].sizi += t[t[x].ch[1]].siz;
t[x].sizi -= t[y].siz;
t[x].siz2i += t[t[x].ch[1]].siz2();
t[x].siz2i -= t[y].siz2();
t[x].ch[1] = y;
pushup(x);
}
}
int findroot(int x)
{
access(x);
Splay(x);
while (t[x].ch[0]) x = t[x].ch[0];
Splay(x);
return x;
}
void link(int x)
{
int y = f[x];
Splay(x);
ans -= t[x].siz2i + t[t[x].ch[1]].siz2();
int z = findroot(y);
access(x);
Splay(z);
ans -= t[t[z].ch[1]].siz2();
t[x].fa = y;
Splay(y);
t[y].sizi += t[x].siz;
t[y].siz2i += t[x].siz2();
pushup(y);
access(x);
Splay(z);
ans += t[t[z].ch[1]].siz2();
}
void cut(int x)
{
int y = f[x];
access(x);
ans += t[x].siz2i;
int z = findroot(y);
access(x);
Splay(z);
ans -= t[t[z].ch[1]].siz2();
Splay(x);
t[x].ch[0] = t[t[x].ch[0]].fa = 0;
pushup(x);
Splay(z);
ans += t[t[z].ch[1]].siz2();
}
void pushup(int x)
{
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].sizi + 1;
}
void add(int u, int v)
{
nxt[++cnt] = head[u];
head[u] = cnt;
to[cnt] = v;
}
void dfs(int u)
{
int i, v;
for (i = head[u]; i; i = nxt[i])
{
v = to[i];
if (v != f[u])
{
f[v] = u;
dfs(v);
}
}
}
1F Nauuo and Bug
题意

给 $a$ 和 $p$,多组询问 $sum(a,l,r,p)$。
数列长度 $10^6$,询问次数 $2\times10^5$,值域 $-10^9$ ~ $10^9$。
题解
区间询问一般采用分块、线段树等方法维护,这些方法都要求我们单独求出较少个区间的答案后进行合并。我们考虑将 Sum 函数改成如下:
int sum(int l, int r, int p, int x) {
for (int i = l; i <= r; ++i)
x = modadd(x, a[i], p);
return x;
}
固定 $p$ 和一个区间,sum 是一个关于 x 的分段函数,可以看出段数为 $O(r-l)$,因为 sum 的结果一定可以写成 $x+s_{l..r}-np$,其中 $s_{l..r}$ 是 $a_{l..r}$ 的区间和,随着 $x$ 的增大,$n$ 不会减小,而 $0 \le n \le r-l+1$,所以段数是线性的。
此时有一个简单的分块做法。将序列分为大小为 $B$ 的 $\frac n B$ 块,每块内预处理出这个块的 sum 函数后用一个存有每段端点的数组记录下来;计算这个函数的方法相当暴力,采用增量法,每次将已有的函数和单点合并后重构每段的起止端点,这将消耗 $O(\frac n B \times B^2=nB)$ 的时间。查询时用二分计算单点上函数的值即可,每次询问的时间是 $O(B+\frac n B \log B)$。认为 $n,q$ 同阶,取 $B=\Theta(\sqrt{n \log n})$ 时复杂度最优为 $O(n \sqrt{n \log n})$。
得到更好的时间复杂度需要一个观察:分段函数中每段的长度都至少是 $P$。证明考虑对区间长度 $n$ 归纳。当 $n=1$ 时由于只有两段,长度均为无穷大,显然;$n>1$ 时考虑将前 $n-1$ 个形成的函数和最后一个合并。详细考虑合并的过程,对于 $f(x)=x+s_{1..n-1}-mP(a \le x \le b)$ 的段,$x + s_{1..n}-mP\ge P \to x \ge (m+1)P-s_{1..n}$ 的部分需要多减一次 $P$,从而会和下一段进行合并。考虑这段函数,减少了一个后缀 $[(m+1)P-s_{1..n},b]$,从上一段合并过来的增加了一段前缀 $[mP-s_{1..n},a]$,新的区间为 $[\min(a,mP-s_{1..n}),\min(b,(m+1)P-s_{1..n}-1]$,简单讨论可知长度仍然不小于 $P$。
我们改为采用线段树维护,查询区间被分解成 $O(\log n)$ 个线段树上区间,假如我们能求出所有线段树上区间的分段函数,即可每次查询 $O(\log^2 n)$ 时间解决。我们求解 $[l..r]$ 的函数时,考虑从 $[l..mid]$ 的函数 $f(x)$ 和 $[mid+1..r]$ 的函数 $g(x)$ 合并而来,合并后的函数即为 $g(f(x))$。我们在的分段函数 $f$ 上按 $x$ 升序扫描,维护 $f(x)$ 对应 $g$ 中的哪一段。当 $x$ 移向 $f$ 中的下一段时,我们从之前 $f(x)$ 的位置暴力移动向新的函数。注意每次移动到下一段 $f(x)$ 只是减 $P$,$f(x)$ 在 $g$ 中的位置会左移,但前面证明过所有段的长度都至少为 $P$,所以 $f(x)$ 的位置只会左移至多一段。当 $x$ 在 $f$ 的同一段中移动时,$f(x)$ 的位置只会右移,从而由均摊分析知道合并的时间是线性的。综上我们在 $O(n \log n+q \log ^2 n)$ 的时间内解决了本题,这是非常优秀的。
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000005;
const ll inf = (ll)1e16;
int n, m, P, a[N];
ll sum[N];
vector<ll> func[N << 2];
vector<ll> merge(int l, int r, int mid, const vector<ll> &f, const vector<ll> &g) {
ll suml = sum[mid] - sum[l - 1], sumr = sum[r] - sum[mid];
vector<ll> ret(f.size() + g.size() - 1, inf);
for (int i = 0, j = 0; i < (int)f.size(); ++i) {
ll xl = f[i], xr = (i + 1 == (int)f.size() ? inf : f[i + 1] - 1), yl = xl + suml - (ll)i * P, yr = xr + suml - (ll)i * P;
while (j > 0 && g[j] > yl) --j;
while (j < (int)g.size() && (j == 0 || g[j] <= yl)) ++j;
--j;
for (; j < (int)g.size() && g[j] <= yr; ++j)
ret[i + j] = min(ret[i + j], max(xl, g[j] - suml + (ll)i * P));
}
ret[0] = -inf;
return ret;
}
void build(int u, int l, int r) {
if (l == r) {
func[u].push_back(-inf);
func[u].push_back(P - a[l]);
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
func[u] = merge(l, r, mid, func[u << 1], func[u << 1 | 1]);
}
ll query(int u, int l, int r, int ql, int qr, ll now) {
if (l >= ql && r <= qr)
return now + sum[r] - sum[l - 1] - (ll)P * (upper_bound(func[u].begin(), func[u].end(), now) - func[u].begin() - 1);
int mid = l + r >> 1;
if (qr <= mid)
return query(u << 1, l, mid, ql, qr, now);
if (ql > mid)
return query(u << 1 | 1, mid + 1, r, ql, qr, now);
return query(u << 1 | 1, mid + 1, r, ql, qr, query(u << 1, l, mid, ql, qr, now));
}
int main() {
scanf("%d%d%d", &n, &m, &P);
for (int i = 1; i <= n; ++i)
scanf("%d", a + i), sum[i] = sum[i - 1] + a[i];
build(1, 1, n);
for (int l, r; m--;) {
scanf("%d%d", &l, &r);
printf("%I64d\n", query(1, 1, n, l, r, 0));
}
return 0;
}

评论正在加载中...如果评论较长时间无法加载,你可以 搜索对应的 issue 或者 新建一个 issue 。