「SDOI2017」树点涂色

LOJ

题目描述

给你一棵有根树，一开始每个点都有不同的颜色。有三种操作：

给定 $x$，将 $x$ 到根的路径修改为一种当前树上没有出现的颜色。
给定 $x$ 和 $y$，询问 $x$ 到 $y$ 的路径上不同颜色的数量。
给定 $x$，令一个点的权值为它到根路径上不同颜色的数量，求子树 $x$ 中的最大权值。

点数和操作数 $10^5$。

简要做法

大致方向肯定是维护每个点到根路径上不同颜色的数量，由于操作 3，用差分维护不太可行，于是锁定为使用线段树以 DFS 序为下标维护每个点到根的颜色数量。如果能够维护这个，操作 2, 3 就好办了：

操作 3 直接区间最大值即可。（子树的 DFS 序连续）
令 $x$ 到根的颜色数量为 $a_x$，那么 $x$ 到 $y$ 的颜色数量为 $a_x+a_y-2a_{lca(x, y)}+1$。这个可以用树上差分来理解。

现在的问题就是如何在进行操作 1 时在线段树上更新每个点到根的颜色数量。

首先，定义“关键点”为根或与 parent 颜色不同的点，那么：

每个点到根的颜色数即为到根路径上的关键点个数。
在操作 1 中，有两类点（下文中也会用“两类点”来指代这两类点）的关键点属性会发生改变：
1. 从 $x$ 到根的路径上，除根外全部变成非关键点。
2. 每个被改变的颜色段，没被改变的那一部分的顶端变为关键点。

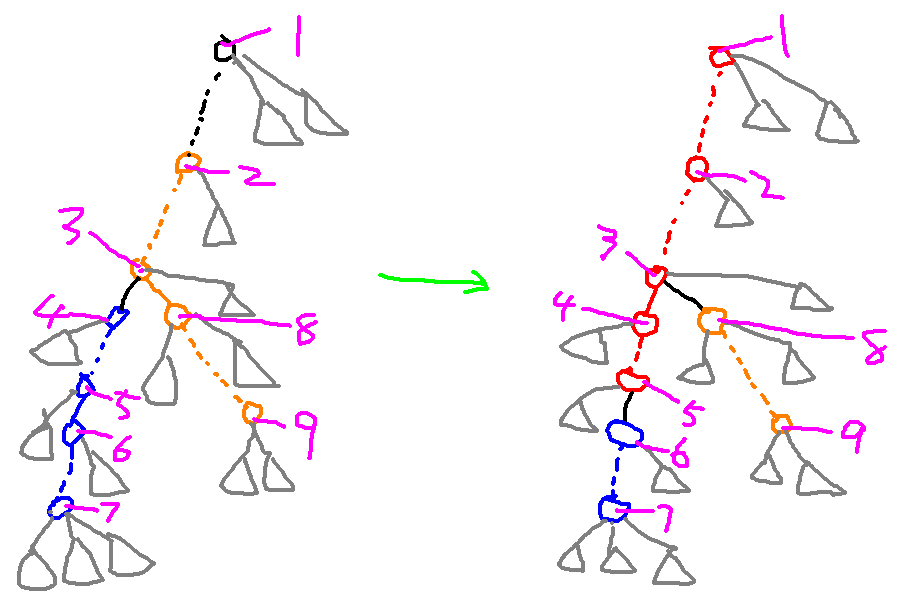
operation1

（P.S. 为啥要用画图（实际上是 KolourPaint 而非 mspaint）而不是 PPT 呢？因为 1. PPT 虽然好看，但手绘貌似更有灵魂 2. 一直用 PPT，想试着换个画风 3. 懒）

在图中，$2$ 和 $4$ 从关键点变成了非关键点，而 $6$ 和 $8$ 从非关键点变成了关键点。

关键点和非关键点的转换其实就是子树加一或减一，于是，问题的关键就在于如何快速找到这两类点。

可以发现，操作 1 其实就和 LCT 的 access 操作是一样的，LCT 中的实链即为本题中颜色相同的段，而使用 LCT 的确能快速找到这两类点（前一类是实链的顶端，即 Splay 中的最小点；后一类是被修改的末端的实儿子，即被修改的末端在 Splay 上的右子树中的最小点），具体怎么找这两类点可以参考下面的代码。

时间复杂度是 $O((n+m)\log^2 n)$（说不定是 $\Theta(n\log n+m\log^2 n)$ 或者 $\Theta(n\log^2 n+m\log n)$，不会算 /kk）。

参考代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <cctype>
#include <algorithm>
#include <functional>

using namespace std;

int read()
{
	int out = 0;
	char c;
	while (!isdigit(c = getchar()));
	for (; isdigit(c); c = getchar()) out = out * 10 + c - '0';
	return out;
}

typedef vector<int> vi;
typedef pair<int, int> pii;

struct SegmentTree
{
#define ls (cur << 1)
#define rs (cur << 1 | 1)
#define mid ((l + r) >> 1)

	vi mx, tag;
	
	SegmentTree(int n, const vi &init) : mx(n * 4), tag(n * 4) { build(1, 1, n + 1, init); }
	
	void pushup(int cur) { mx[cur] = max(mx[ls], mx[rs]); }
	
	void build(int cur, int l, int r, const vi &init)
	{
		if (l == r - 1) mx[cur] = init[l];
		else
		{
			build(ls, l, mid, init);
			build(rs, mid, r, init);
			pushup(cur);
		}
	}
	
	void modify(int cur, int x)
	{
		mx[cur] += x;
		tag[cur] += x;
	}
	
	void pushdown(int cur)
	{
		modify(ls, tag[cur]);
		modify(rs, tag[cur]);
		tag[cur] = 0;
	}
	
	void modify(int cur, int l, int r, int L, int R, int x)
	{
		if (l >= R || r <= L) return;
		if (L <= l && r <= R) modify(cur, x);
		else
		{
			pushdown(cur);
			modify(ls, l, mid, L, R, x);
			modify(rs, mid, r, L, R, x);
			pushup(cur);
		}
	}
	
	int query(int cur, int l, int r, int L, int R)
	{
		if (l >= R || r <= L) return 0;
		if (L <= l && r <= R) return mx[cur];
		pushdown(cur);
		return max(query(ls, l, mid, L, R), query(rs, mid, r, L, R));
	}

#undef ls
#undef rs
#undef mid
};

struct LCT
{
	struct Node
	{
		vi ch;
		int pa;
		Node() : ch(2), pa(0) {}
	};
	
	vector<Node> t;
	
	LCT(int n) : t(n + 1) {}
	
	bool nroot(int x) { return x == t[t[x].pa].ch[0] || x == t[t[x].pa].ch[1]; }
	
	void rotate(int x)
	{
		int y = t[x].pa;
		int z = t[y].pa;
		int k = x == t[y].ch[1];
		if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
		t[x].pa = z;
		t[y].ch[k] = t[x].ch[k ^ 1];
		t[t[x].ch[k ^ 1]].pa = y;
		t[x].ch[k ^ 1] = y;
		t[y].pa = x;
	}
	
	void Splay(int x)
	{
		while (nroot(x))
		{
			int y = t[x].pa;
			int z = t[y].pa;
			if (nroot(y)) rotate((x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? x : y);
			rotate(x);
		}
	}
	
	int gettop(int x)
	{
		while (t[x].ch[0]) x = t[x].ch[0];
		return x;
	}
	
	vector<pii> access(int x) // 返回值为每一对“两类点”
	{
		vector<pii> res;
		for (int y = 0; x; x = t[y = x].pa)
		{
			Splay(x);
			res.emplace_back(gettop(x), gettop(t[x].ch[1]));
			t[x].ch[1] = y;
		}
		return res;
	}
};

int main()
{
	int n = read();
	int m = read();
	
	vector<vi> g(n + 1);
	
	for (int i = 1; i < n; ++i)
	{
		int u = read();
		int v = read();
		g[u].push_back(v);
		g[v].push_back(u);
	}
	
	LCT lct(n);
	int dfntot = 0;
	vi dfn(n + 1), exi(n + 1), pa(n + 1), son(n + 1), siz(n + 1), dep(n + 1), tp(n + 1);
	
	function<void(int)> dfs1 = [&](int u)
	{
		siz[u] = 1;
		dfn[u] = ++dfntot;
		for (auto v : g[u])
		{
			if (v == pa[u]) continue;
			dep[v] = dep[u] + 1;
			lct.t[v].pa = u;
			pa[v] = u;
			dfs1(v);
			siz[u] += siz[v];
			if (siz[v] > siz[son[u]]) son[u] = v;
		}
		exi[u] = dfntot;
	};
	
	function<void(int)> dfs2 = [&](int u)
	{
		if (!son[u]) return;
		tp[son[u]] = tp[u];
		dfs2(son[u]);
		for (auto v : g[u])
		{
			if (v == pa[u] || v == son[u]) continue;
			tp[v] = v;
			dfs2(v);
		}
	};
	
	auto lca = [&](int u, int v)
	{
		while (tp[u] != tp[v])
		{
			if (dep[tp[u]] > dep[tp[v]]) u = pa[tp[u]];
			else v = pa[tp[v]];
		}
		return dep[u] > dep[v] ? v : u;
	};
	
	dep[1] = tp[1] = 1;
	dfs1(1);
	dfs2(1);
	
	vi init(n + 1);
	for (int i = 1; i <= n; ++i) init[dfn[i]] = dep[i];
	SegmentTree seg(n, init);
	
	while (m--)
	{
		switch(read())
		{
			case 1:
			{
				int x = read();
				lct.Splay(x);
				auto res = lct.access(x);
				for (auto p : res)
				{
					int u = p.first;
					int v = p.second;
					if (u != 1) seg.modify(1, 1, n + 1, dfn[u], exi[u] + 1, -1);
					if (v) seg.modify(1, 1, n + 1, dfn[v], exi[v] + 1, 1);
				}
				break;
			}
			case 2:
			{
				int x = read();
				int y = read();
				int u = lca(x, y);
				int ans = seg.query(1, 1, n + 1, dfn[x], dfn[x] + 1);
				ans += seg.query(1, 1, n + 1, dfn[y], dfn[y] + 1);
				ans -= 2 * seg.query(1, 1, n + 1, dfn[u], dfn[u] + 1);
				ans += 1;
				printf("%d\n", ans);
				break;
			}
			case 3:
			{
				int x = read();
				printf("%d\n", seg.query(1, 1, n + 1, dfn[x], exi[x] + 1));
				break;
			}
		}
	}
	
	return 0;
}

~~（没有全局变量的代码是不是非常清爽）~~

文章目录

简要做法

参考代码