遗传病概率计算中的条件概率问题
文章目录
【注意】最后更新于 January 10, 2021,文中内容可能已过时,请谨慎使用。
考试中的一道遗传图谱计算题为何会引发整整一周的争论?
为何办公室中只有数学老师认为题目有问题?
为何数学老师觉得参考答案错了却算不出正确答案?
后发生的事能“影响”先发生的事的概率吗?
遗传图谱计算中的“概率”意义究竟是什么?
如果高考有这样的题,我们在考场上应该怎么做?考完了应该骂出题人吗?
题目
由于我没有把卷子带回家,就没有放这次考试中的题,而是在网上找了一道类似的题:
题目描述
下面是某家族单基因遗传病系谱图,基因用 $\rm A$、$\rm a$ 表示。请据图回答:$\rm{II}_2$ 的基因型概率是多少?
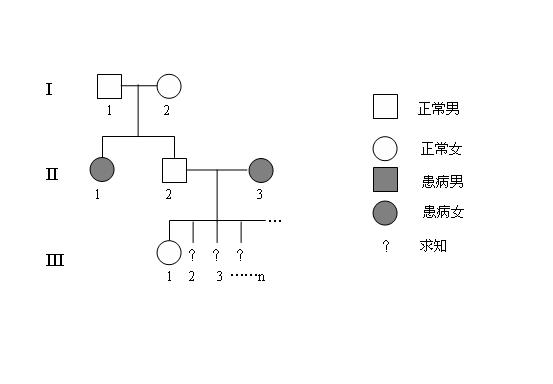
一个解法
我的解法和 陈宝明.遗传概率的一个认识误区.生物学通报.2007(02) 大体相同,我就不再赘述了。
描述这个解法的其它文章还有很多,但很多不方便从知网上下载 🌚️。我下载到了两篇:
这些文章中也有提及常见的那种错误解法,即一路顺推不管已知的后代对前面未知基因型的影响。
一些争论
因为大家都是学过条件概率的高中生,我本以为我简单解释一下大家就都能理解,但事实却并非如此。(于是我才会想来写这篇博客。)
后代不会影响亲本
“后代不会影响亲本”是一个很多人都这么认为但根本站不住脚的观点。除非你认为,在上面的例题中,即使 $\rm{III}_1$ 是患病的,$\rm{II}_2$ 的基因型依然有可能是 $\rm{AA}$。
“推断”其实就是一种特殊的“影响概率”,只不过是把概率影响成了一个 01 分布。
如果你承认“$\rm{III}_1$ 患病”可以推出“$\rm{II}_2$ 的基因型是 $\rm{Aa}$”,而不承认“$\rm{III}_1$ 不患病”影响“$\rm{II}_2$ 的基因型是 $\rm{Aa}$”的概率,那就相当于:告诉你一个骰子的点数是奇数,你承认它的点数不是 6;告诉你它的点数是偶数,你却依然认为它的点数是 6 的概率是 $\frac{1}{6}$。
另外就是,虽然持这种观点的人(在我们班上,以及网上,还有参考答案中)很多,但可能是由于我不知道这种文章的标题应该长啥样,我并没有搜到支持这种观点的文章。
个体的基因型是特定的
这位丁志芳直接写了三篇文章从不同的角度批判了这种计算方式:
乍一看觉得很吓人,但这三篇文章说来说去都是一回事(其实我并没有细看,就扫了一眼看了下总结),并不是觉得后代不会影响亲本,而是认为“个体的基因型是特定的”:论基因型的特定性。
这个观点是有一些道理的。在讨论之前,我们首先要明白,我们所说的“概率”究竟是什么,否则就是在不同的论点上针锋相对了。
在丁志芳看来,遗传图谱描述的是一个真实存在的家族,其中每个人的基因型都是特定的,而“概率”只适用于未出生的孩子,不适用于已存在的个体。丁志芳的矛头指向的不只是本文讨论的这种有较大争议的题目,而是一切把已存在的个体卷入概率计算的题目。丁志芳认为,这种情况下,不应该说概率是“多少”,而是应该说概率是“多少或多少”,即对已存在个体的每种情况分别讨论。
在这种观点下,“概率”其实就是豌豆杂交实验中的“性状比”。这样的话,我们的确不能把已存在个体的多种可能的基因型放在一起计算:一个亲本有 $\frac{1}{2}$ 的概率是 $\rm{AA}$,有 $\frac{1}{2}$ 的概率是 $\rm{Aa}$,另一个亲本是 $\rm{aa}$,但他们的后代并不会是 $\frac{1}{4}$ 患病,而是有 $\frac{1}{2}$ 的概率全不患病,有 $\frac{1}{2}$ 的概率有一半患病。听说有同学认为“这是在不犯错误的情况下的把握而不能等同于概率”,或许他对“概率”的理解也大致如此。
但是,正如每次投骰子时投出的点数都是特定的而我们依然可以讨论骰子投到某个点数的概率,我们在不知道已存在个体的基因型时,也可以计算其概率。或者说,我们可以把“概率”视作“后代性状比例”的期望值。
总之,这个争论的重点在于“概率”究竟是什么,是个比较哲学的问题 🌚️。但是如果你支持这个观点,那一切把已存在的个体卷入概率计算的题目你都不用做了。
结论
认为“知道后代对亲本完全没有影响”,即在本文开头给出的题目中认为“无论后代如何,$\rm{II}_2$ 的基因型都是 $\frac{1}{3}\rm{AA}$, $\frac{2}{3}\rm{Aa}$”,这肯定是不正确的。
如果你愿意的话,你还可以支持 丁志芳的观点:凡是把已存在的个体卷入概率计算的都是错的,这道题只要答案是单个数字就是错的。
高考题
这种题高考不会有吧。
虽然不知道以后的高考会不会有,但以前的高考真的有,而且答案还是错的 🌚️
如果以后高考真的还有这种题,只能祝大家好运了。(如果答案是错的记得骂出题人)

评论正在加载中...如果评论较长时间无法加载,你可以 搜索对应的 issue 或者 新建一个 issue 。